こんにちは．高山です．
以前の記事 (1, 2)で，動作追跡点の欠損値を線形補間で穴埋めする方法を紹介しました．
こちらの記事の記事では，Numpyの線形補間関数 interp を用いた実装を紹介しましたが，今回は，処理を行列計算で実装して高速化を行う方法を紹介します．
今回解説するスクリプトはGitHub上に公開しています．

この方法はTensorflowやPyTorchなどでも実装可能です．
他のライブラリを用いた実装方法は後日別記事で紹介したいと思います．

本記事の実装方法は，Brent M. Spell氏のブログに記載の方法を参考にしています．
この度，本記事向けに拡張したコードを記載してよいかお伺いしたところ，快く許可してくださいました．
この場を借りて感謝申し上げます．

更新履歴 (大きな変更のみ記載しています)

• 2024/09/17: タグとサマリを更新しました
• 2023/10/30: 処理時間の計測方法を更新しました

1. 高速化の考え方

今回紹介する方法では，Numpyの演算機能を用いて複数の追跡点と特徴量の補間処理を同時に行います．

これにより次の2点で高速化が行なえます．

1. 時間のかかるPythonのforループや冗長な処理を削除
2. C言語やCUDA (TensorflowなどでGPU利用時) などの高速な実装を利用

例えば，ベクトルや行列\(A\)があった場合，\(2 * A\)をPythonの標準機能だけで実装しようとすると，forループを回す必要があります．
Pythonなどのスクリプト言語のforループは速度が遅いことが知られています．
一方，Numpyで同様の処理を行う場合には b = 2 * A のようにシンプルにコードが書け，かつ，内部ではC言語などで実装された高速な処理が動作します．
また，Tensorflowなどの機械学習用ライブラリを用いる場合は，GPUの並列処理を用いることも可能です．

2. まずは簡単な例で図解

まずは簡単な例を用いて図と数式を使って説明したいと思います．
少し長くなりますので，コードを眺めた方が理解が早いという方は第3節に進んでいただいて構いません．

2.1 やりたいこと

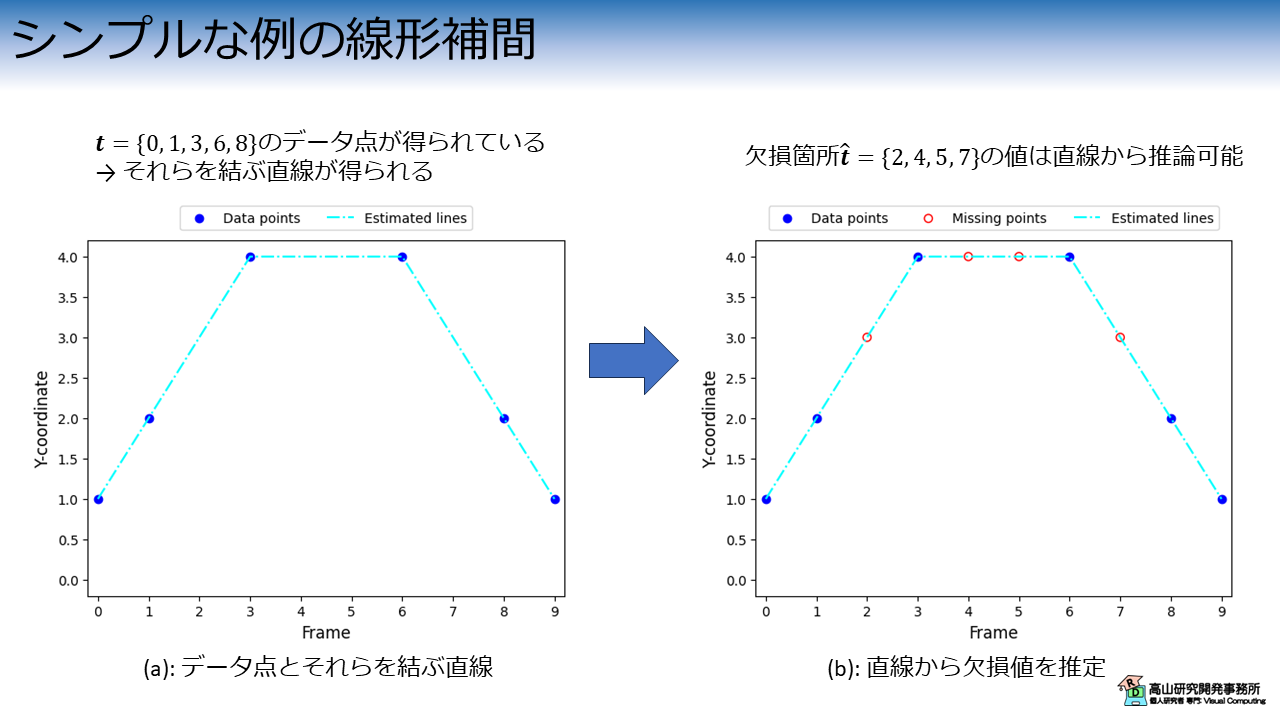
まず，6個のデータ点 \((\boldsymbol{t}, \boldsymbol{y}) = \{(0, 1), (1, 2), (3, 4), (6, 4), (8, 2), (9, 1)\}\) が得られているとします．
図1(a) に示すように，これら6個のデータ点からは隣接点間を結ぶ直線を求めることができます．
そして図1(b)に示すように，補間したい点の\(t\)座標 \(\hat{\boldsymbol{t}}=\{2, 4, 5, 7\}\) が定まればこれらの値から欠損値を求めることができます．
これが今やりたいことで，今回はNumpyの補間関数やループの逐次処理に頼ることなく，行列データの演算で処理していきます．

2.2 直線の傾きベクトル\(\boldsymbol{\alpha}\)を求める

座標値をベクトル形式で並べる

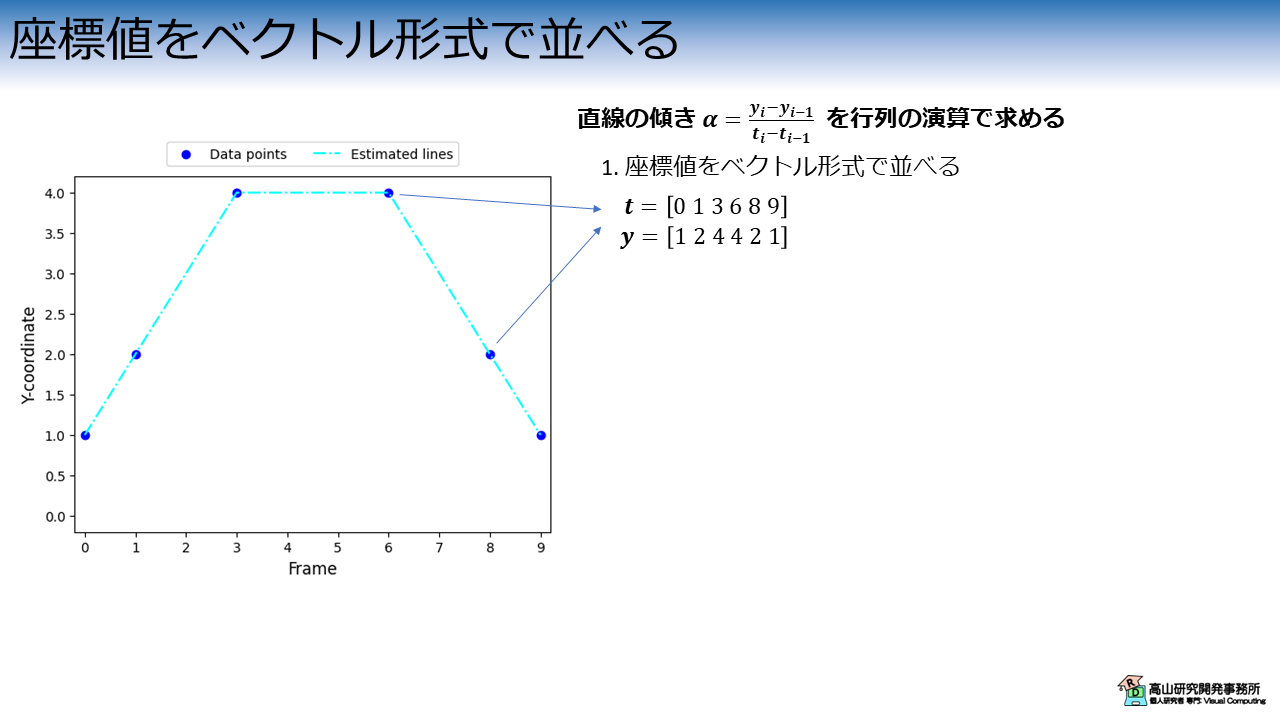
まず最初に，直線の傾きベクトル\(\boldsymbol{\alpha}\)を求めるために，座標値をベクトル形式で並べます．
例えば今回の例の場合，図2に示すように動画フレームのインデクスと \(y\) 座標値のベクトルはそれぞれ下記のようになります．

• \(\boldsymbol{t}=[0\ 1\ 3\ 6\ 8\ 9]\)
• \(\boldsymbol{y}=[1\ 2\ 4\ 4\ 2\ 1]\)

先頭と末尾にダミー値を追加

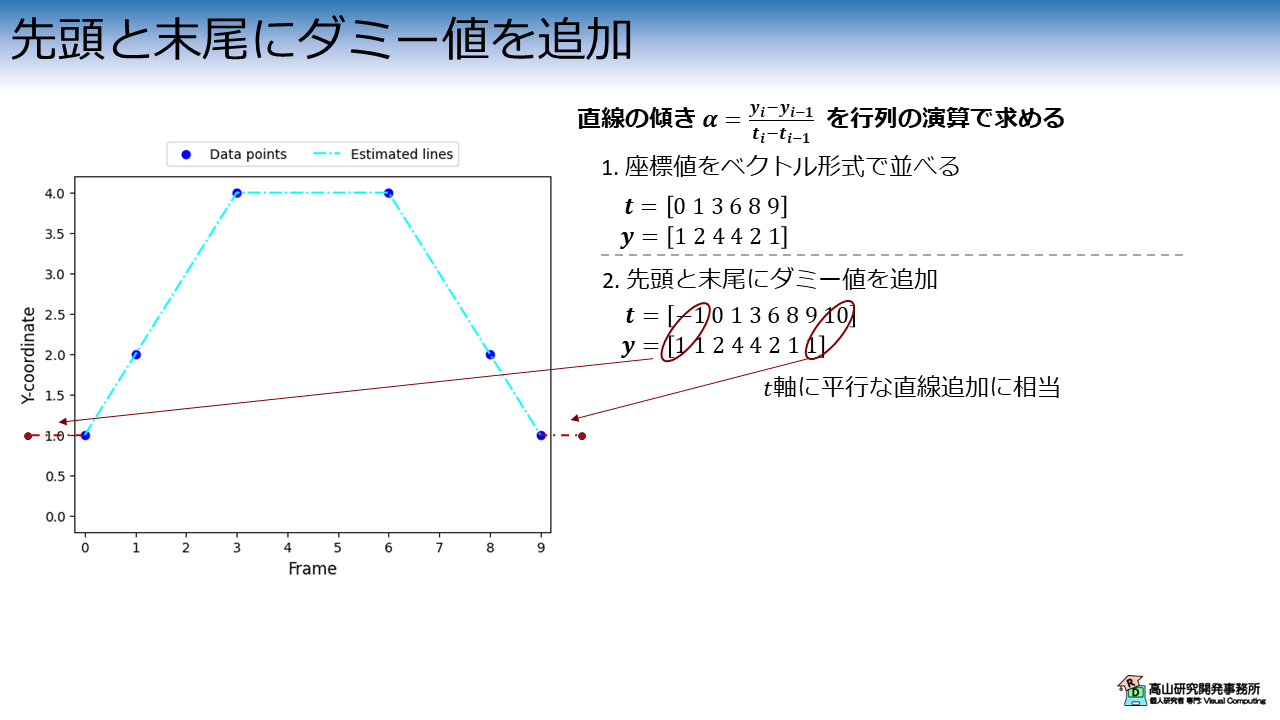
次に，図3に示すようにそれぞれのベクトルの先頭と末尾にダミー値を追加します．
これは，\(t\) 軸に平行な直線を追加する操作に相当します．
このようにすることで，分岐処理を入れることなく端点の直線パラメータを求めることができます．

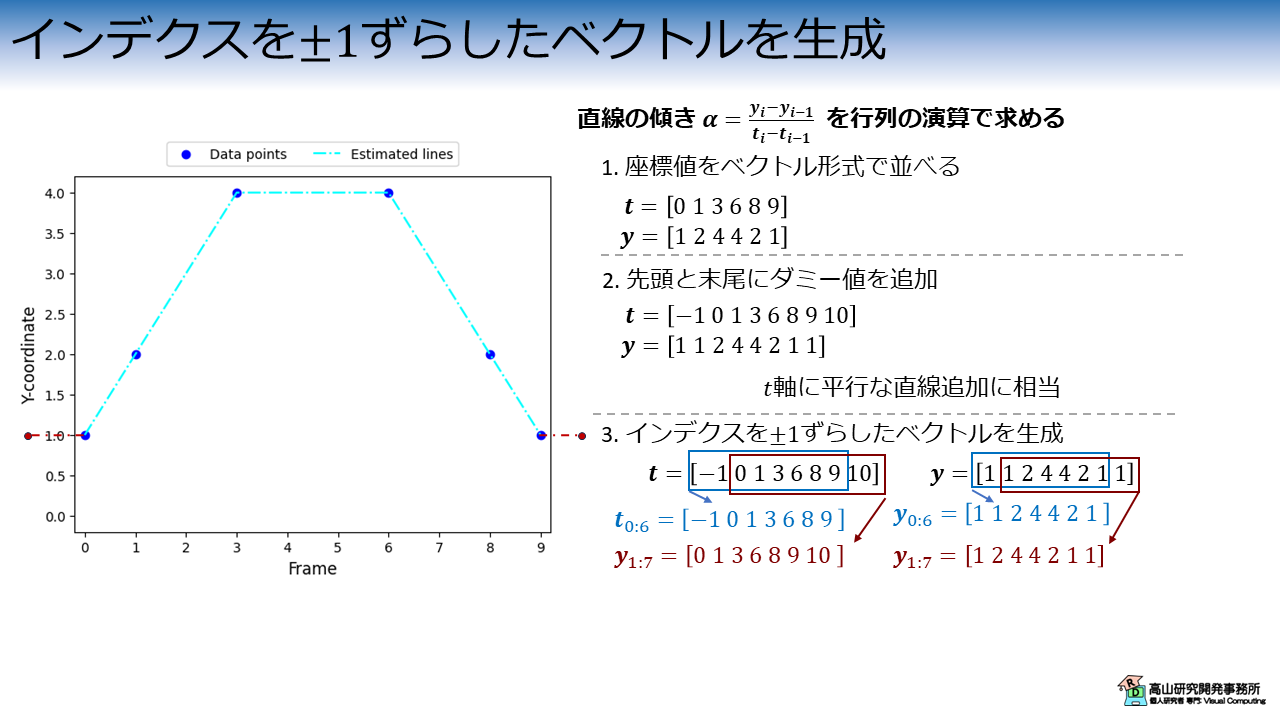
インデクスを ± 1 ずらしたベクトルを生成

その後，図4に示すようにそれぞれのベクトルからインデクスを\(\pm{1}\)ずらしたベクトルを生成します．
この操作で，\(\alpha\) の演算に用いる \(t_i, t_{i-1}, y_i, y_{i_1}\) を作成しています．

直線の傾きベクトル α を算出

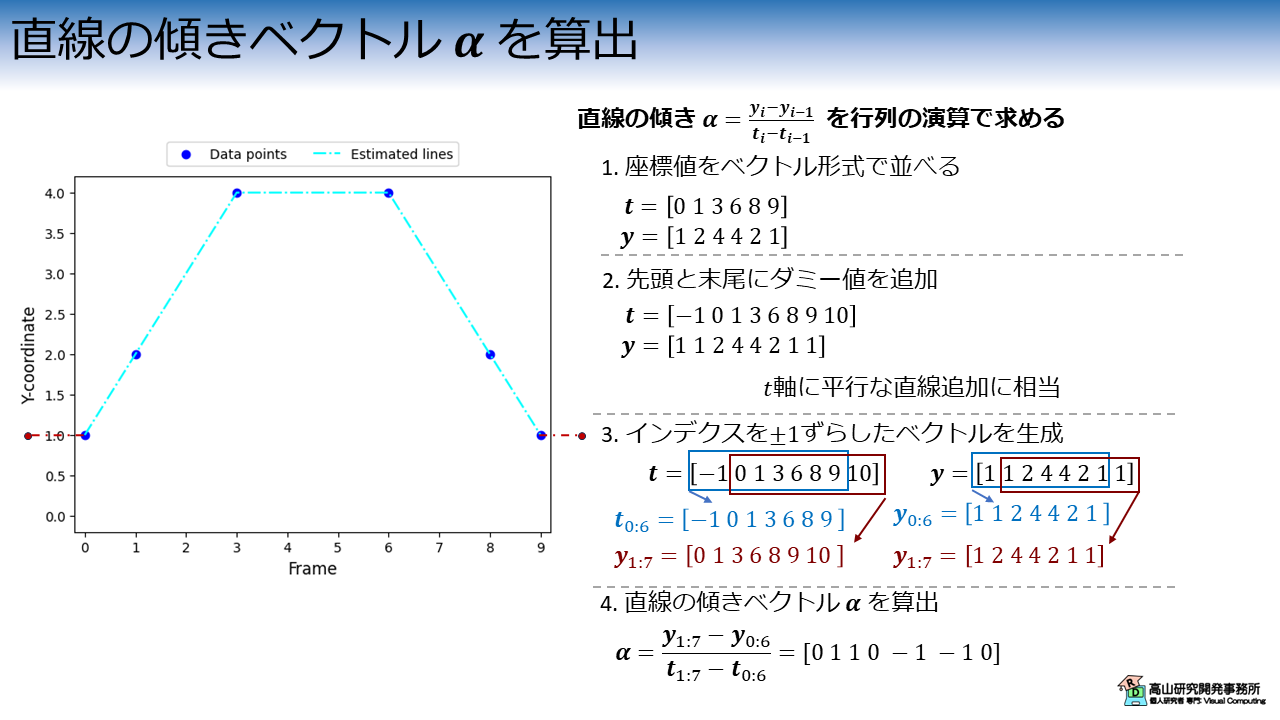
最後に，図5に示すように \(\boldsymbol{\alpha}=(\boldsymbol{y}_{1:7} - \boldsymbol{y}_{0:6}) / (\boldsymbol{t}_{1:7} - \boldsymbol{t}_{0:6})\) を計算して直線の傾きベクトル \(\boldsymbol{\alpha}\) を算出します．
今回の例では，\(\boldsymbol{\alpha}=[0\ 1\ 1\ 0\ -1\ -1\ 0]\) になります．

2.3 切片のベクトル\(\boldsymbol{\beta}\)を求める

α の末尾削除 & ダミー値を追加

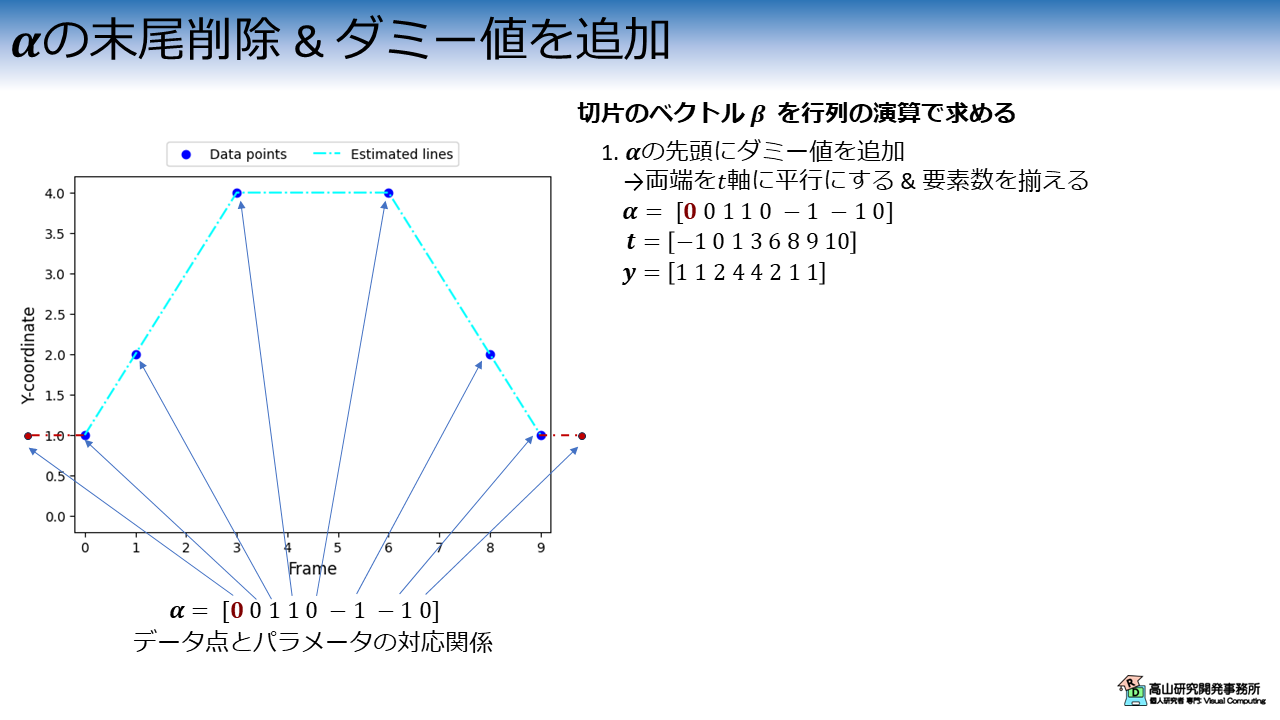
\(\boldsymbol{\alpha}\) が求まったので，次に直線の切片ベクトル \(\boldsymbol{\beta}\) を求めます．
\(\boldsymbol{\alpha}\) は \(\boldsymbol{t}\) や \(\boldsymbol{y}\) よりも要素が1個少ないため，先頭にダミー値を追加して要素数を揃えます．
ここでは，両端を \(t\) 軸に平行にしたいので \(0\) を加えています．
この操作により，図6左側のグラフに示すようにデータ点と直線パラメータが1対1で対応するようになります．

切片のベクトル β を求める

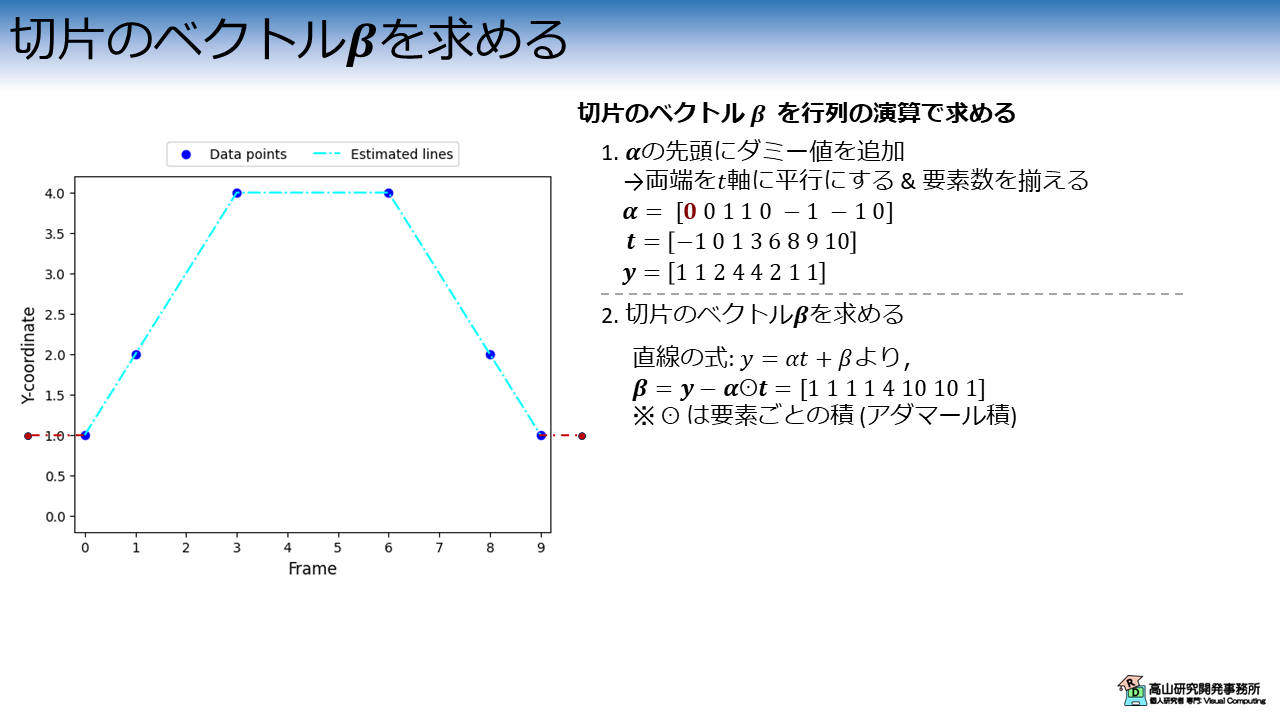
直線の切片ベクトル \(\boldsymbol{\beta}\) を求めます．
図7に示すように，直線の式 \(y=\alpha t + \beta\) より \(\beta = y - \alpha t\) なので，直線の切片ベクトル \(\boldsymbol{\beta}\) は次のように求まります．

\(\boldsymbol{\beta} = \boldsymbol{y} - \boldsymbol{\alpha} \odot \boldsymbol{t} = [1\ 1\ 1\ 1\ 4\ 10\ 10\ 1]\)

ここで，\(\odot\) は要素毎の積を示します (アダマール積と言います)．

2.4 線形補間の実行

ここまでの処理で，データ点の直線パラメータを算出することができました．
これらの値を用いて線形補間を行います．

補間点のパラメータを求める

まず，補間対象の点 (以下，補間点) を算出するための直線パラメータを求めます．
図8左側のグラフを見ると直ぐに分かると思いますが，補間点と同一直線上にあるデータ点のパラメータ，つまり，自身の直後 (直前でも良いです) のデータ点のパラメータを用いれば良いです．

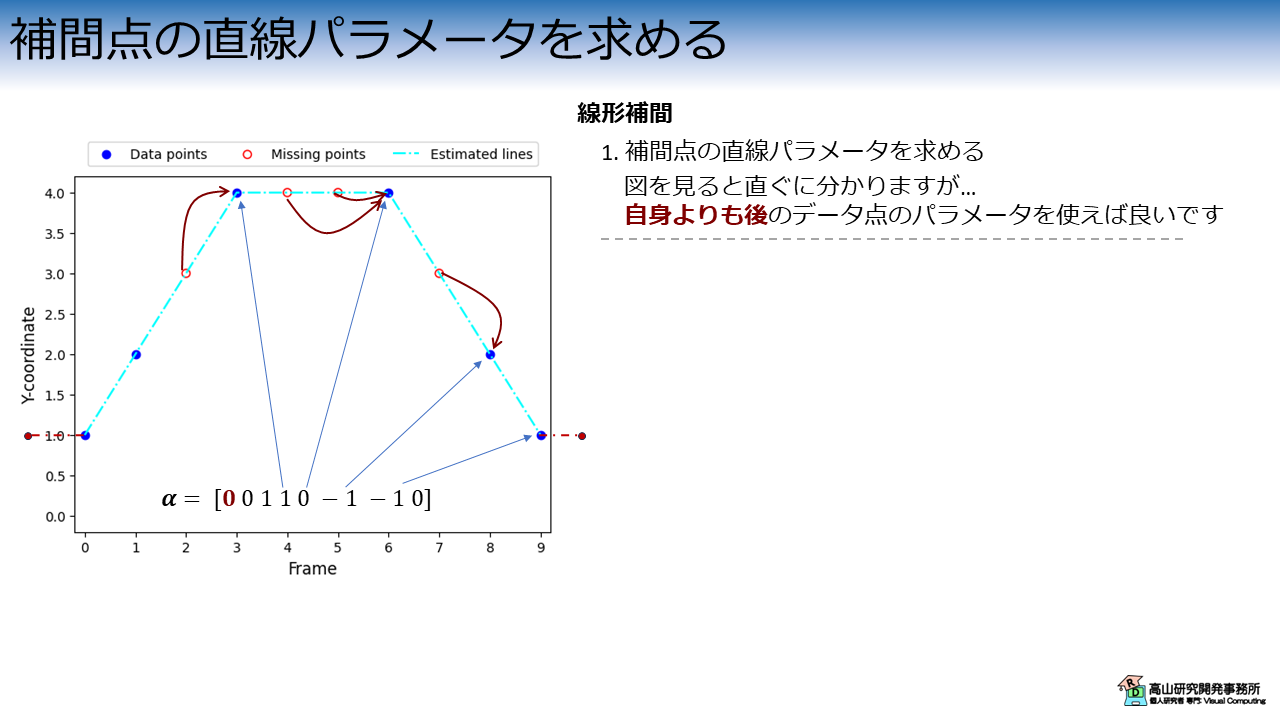
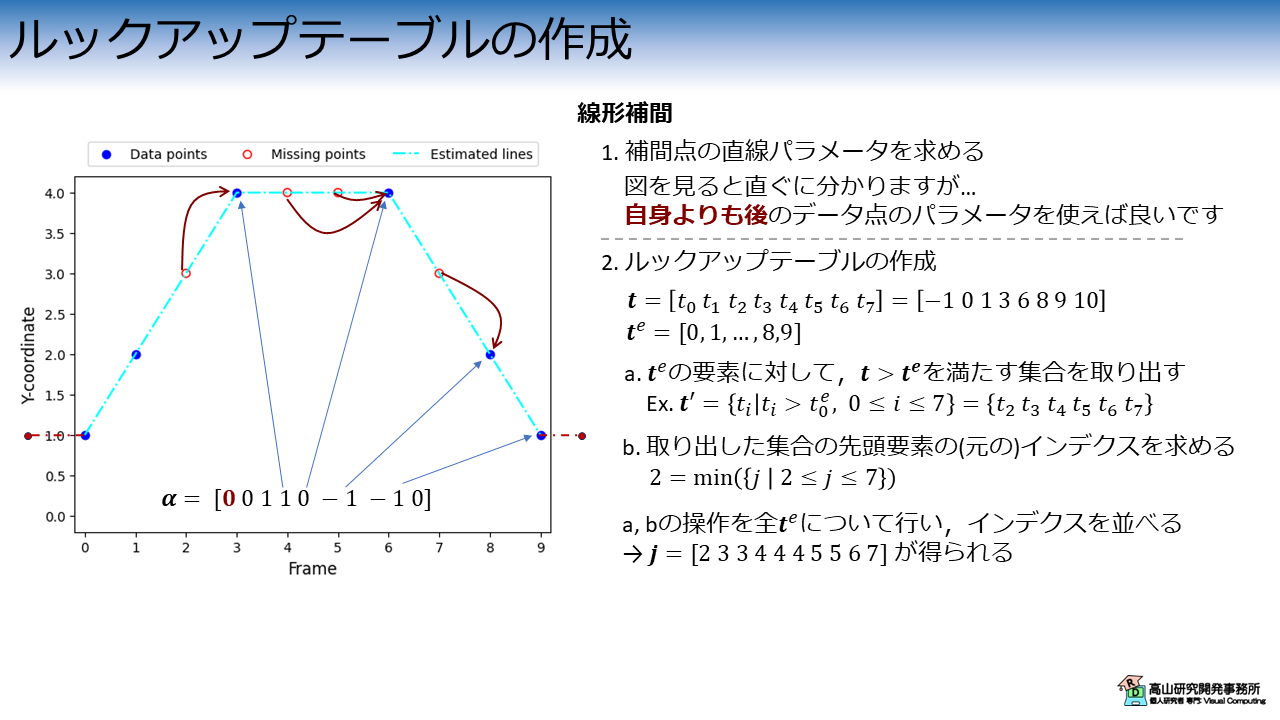
ルックアップテーブルの作成

上記を実現するために，動画フレームインデクス \(t\) とデータ点インデクスのマッピングを表すルックアップテーブルを作成します．
今実現したいことは，"\(t=0\) の場合は2番目のデータ点のパラメータを用いる"，"\(t=1\) の場合は3番目のデータ点のパラメータを用いる"，という処理です．
これを行うために，\(t\) の全要素に対して \([2\ 3\ ...]\) というインデクス配列を求めます．

操作は図9右側に示すとおりです．
まず，\(t\) の全要素をベクトルで並べて \(\boldsymbol{t}^e = [0\ 1\ \ldots \ 8\ 9]\) とします．
次に，\(\boldsymbol{t}^e\) の各要素に対して \(\boldsymbol{t} > \boldsymbol{t}^e\) を満たす集合を取り出します．
例えば，\(t^e_0 = 0\) に対しては次のような集合が求まります．

\(\boldsymbol{t}^{'} = \{ t_i \ |\ t_i > t^e_0,\ 0 \leq i \leq 7 \} = \{ t_2, t_3, t_4, t_5, t_6, t_7 \}\)

取り出した集合に対して先頭要素の (元の) インデクスを求めると，次のようになります．

\(2 = \min (\{ j \ |\ 2 \leq j \leq 7 \})\)

上記の操作を \(\boldsymbol{t}^e\) の全要素に対して行い，得られた配列をベクトルとして並べると \(\boldsymbol{j} = [2\ 3\ 3\ 4\ 4\ 4\ 5\ 5\ 6\ 7]\) が求まります．

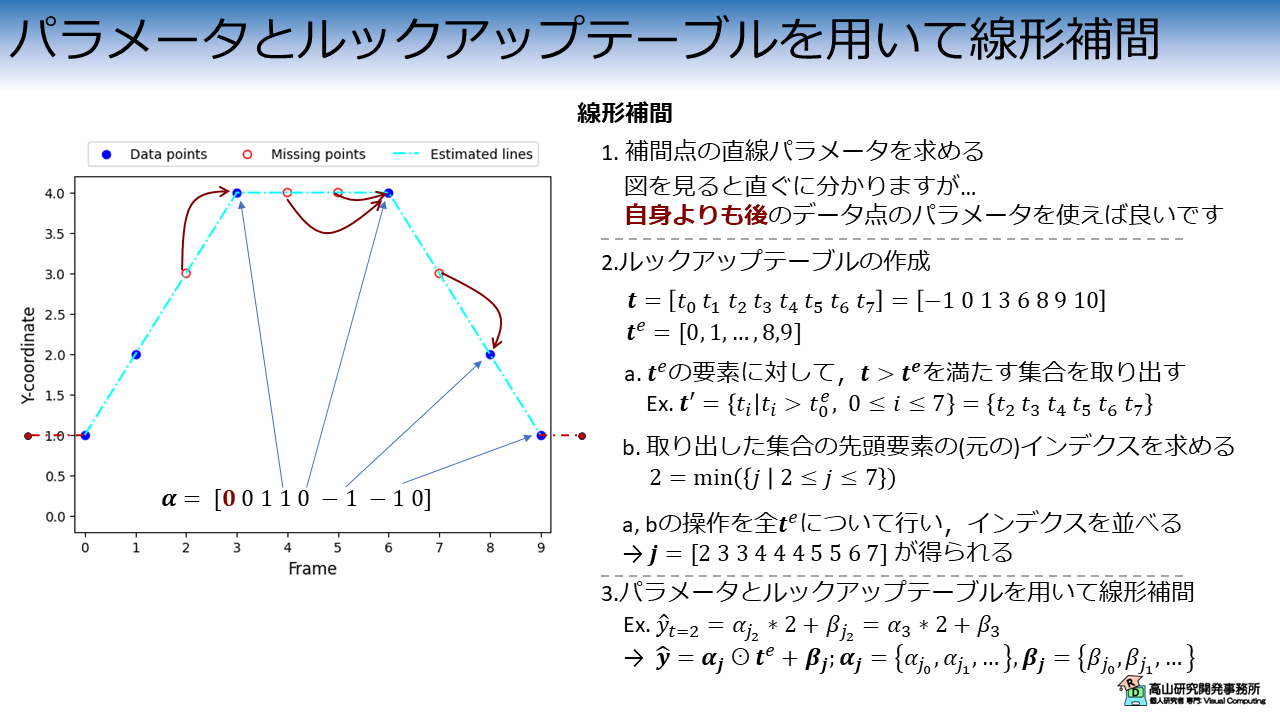
パラメータとルックアップテーブルを用いて線形補間

求めた直線パラメータとルックアップテーブルを用いて線形補間を行います．
例えば，\(t=2\) の補間点の \(y\) 座標は下記のようにして求めることができます．

\(\hat{y}_{t=2} = \alpha_{j_2} * 2 + \beta_{j_2} = \alpha_3 * 2 + \beta_3\)

直線パラメータとルックアップテーブルはベクトルなので，下記のようにベクトルの演算で全ての補間点 (とデータ点) の \(y\) 座標値を一度に求めることができます．

\(\hat{\boldsymbol{y}} = \boldsymbol{\alpha_{j}} \odot \boldsymbol{t}^e + \boldsymbol{\beta_{j}}\),
\(\boldsymbol{\alpha_{j}} = \{ \alpha_{j_0}, \alpha_{j_1}, \ldots \},\ \boldsymbol{\beta_{j}} = \{ \beta_{j_0}, \beta_{j_1}, \ldots \}\)

行列の演算で線形補間を行う方法の説明は以上です．

複数系列を同時に補間するには?

ここでは説明のために，1系列のデータ点をベクトルで表して補間を行いました．
複数の系列 (例えば複数の追跡点や複数の特徴量など) に対しては，\(\boldsymbol{t}\) と \(\boldsymbol{y}\) を系列分並べて，データを行列で持ち同様の操作を行うことで同時に補間を行うことができます．

データを行列形式で並べるためには，各系列のデータ点数が同じである必要があります．
同一追跡点の特徴量 (\(x, y, z, c\) など) は常にこの条件を満たしています．

また，追跡にMediaPipeを用いる場合，追跡失敗時は部位単位 (顔，手，身体など) でデータが欠落します．
同一部位の追跡点系列のデータ点数は常に同じになるため，多くても4回処理を行えば全追跡点の補間が行なえます．

次節からは，実際に複数系列を同時に線形補間する処理の実装例を紹介します．

3. 実装の紹介

3.1 モジュールのロード

まず最初に，下記のコードでモジュールをロードします．

1
2
3
4
5
6
7
8

# Standard modules.
import gc
import sys
import time
from functools import partial

# CV/ML.
import numpy as np

【コード解説】
- 標準モジュール
  - gc: ガベージコレクション用ライブラリ
    処理時間計測クラスの内部処理で用います．
  - sys: Pythonシステムを扱うライブラリ
    今回はバージョン情報を取得するために使用しています．
  - time: 時刻データを取り扱うためのライブラリ
    今回は処理時間を計測するために使用しています．
  - functools: 関数オブジェクトを操作するためのライブラリ
    処理時間計測クラスに渡す関数オブジェクト作成に使用しています．
- 画像処理・機械学習向けモジュール
  - numpy: 行列演算ライブラリ

記事執筆時点のPythonと主要モジュールのバージョンは下記のとおりです．

1
2

print(f"Python:{sys.version}")
print(f"Numpy:{np.__version__}")

Python:3.10.12 (main, Jun 11 2023, 05:26:28) [GCC 11.4.0]
Numpy:1.23.5

3.2 入力データのロード

次に，下記の処理で補間前と補間後の追跡点データをダウンロードします．
補間後の追跡点データは以前の記事で紹介した処理で生成したデータです．
このデータは今回の処理で生成したデータとの比較に用います．

!wget https://github.com/takayama-rado/trado_samples/raw/main/test_data/finger_far0_non_static.npy
!wget https://github.com/takayama-rado/trado_samples/raw/main/test_data/finger_far0_non_static_interp.npy

ls コマンドでデータがダウンロードされているか確認します．

!ls
finger_far0_non_static_interp.npy  finger_far0_non_static.npy  sample_data

次のコードでは，追跡点をロードして，関数の仕様に合わせて形状を変更しています．
追跡点データは[P, T, J, C]形状 (Pは人物インデクス) の配列ですが，人物は1名だけですのでP軸は除去しています．

1
2
3
4
5
6
7

# Load data.
trackdata = np.load("finger_far0_non_static.npy")
reftrack = np.load("finger_far0_non_static_interp.npy")

# Remove person axis.
trackdata = trackdata[0]
reftrack = reftrack[0]

3.3 実験用処理の実装

実験に先立って，処理時間計測用の関数と実験用定数を定義します．
次のコードは処理時間の値から，適切なSI接頭辞を設定し，文字列にして返します．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

def get_perf_str(val):
    token_si = ["", "m", "µ", "n", "p"]
    exp_si = [1, 1e3, 1e6, 1e9, 1e12]
    perf_str = f"{val:3g}s"
    si = ""
    sval = val
    for token, exp in zip(token_si, exp_si):
        if val * exp > 1.0:
            si = token
            sval = val * exp
            break
    perf_str = f"{sval:3g}{si}s"
    return perf_str

- 引数
  - val: 処理時間を示す値 (秒)
- 2-6行目: 変数の初期化
- 7-11行目: 接頭辞を選択して，表示値を調整
- 12行目: 表示文字列を作成

次のコードは，処理時間を格納した配列から統計量を求めて表示します．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

def print_perf_time(intervals, top_k=None):
    if top_k is not None:
        intervals = np.sort(intervals)[:top_k]
    min = intervals.min()
    max = intervals.max()
    mean = intervals.mean()
    std = intervals.std()

    smin = get_perf_str(min)
    smax = get_perf_str(max)
    mean = get_perf_str(mean)
    std = get_perf_str(std)
    if top_k:
        print(f"Top {top_k} summary: Max {smax}, Min {smin}, Mean +/- Std {mean} +/- {std}")
    else:
        print(f"Overall summary: Max {smax}, Min {smin}, Mean +/- Std {mean} +/- {std}")

- 引数:
  - intervals: 処理時間のNumpy配列
  - top_k: intervalsから，処理時間が短いサンプルをk個取り出して統計量を算出
- 2-3行目: Top K個のサンプル抽出
- 4-7行目: 統計量算出
- 9-16行目: 表示文字列を作成して表示

次のクラスは，入力した関数を複数回呼び出して，処理時間の統計量を表示します．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class PerfMeasure():
    def __init__(self,
                 trials=100,
                 top_k=10):
        self.trials = trials
        self.top_k = top_k

    def __call__(self, func):
        gc.collect()
        gc.disable()
        intervals = []
        for _ in range(self.trials):
            start = time.perf_counter()
            func()
            end = time.perf_counter()
            intervals.append(end - start)
        intervals = np.array(intervals)
        print_perf_time(intervals)
        if self.top_k:
            print_perf_time(intervals, self.top_k)
        gc.enable()
        gc.collect()

- 引数:
  - trials: 入力関数の実行回数
  - top_k: 値が定義されている場合，全体の処理時間配列から処理時間が短いサンプルをk個取り出して統計量を算出
- 9-10行目: 計測中はガベージコレクションをしないように設定
- 11-20行目: 処理時間計測処理
- 21-22行目: ガベージコレクションの設定を元に戻す

最後に，次のコードで実験用の定数を定義して処理時間計測クラスをインスタンス化しています．

1
2
3

TRIALS = 100
TOPK = 10
pmeasure = PerfMeasure(TRIALS, TOPK)

実際の所，Colabの様な複雑な処理環境で他のプロセスの影響を排除して純粋な処理時間を計測するのはかなり難しいです．
そこでここでは，処理の繰り返し数を \(100\) とし全体の統計量に加えて，処理時間の短い代表値 \(10\) 試行からも統計量を表示するようにしています．

3.4 補間処理

ここから先は補間処理の実装・実行を行います．

補間処理の実装

次のコードでは，第2節で説明した行列計算を用いた線形補間処理を実装しています．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

def matrix_interp(track):
    orig_shape = track.shape
    tlength = orig_shape[0]
    mask = track[:, 0, -1] != 0
    valid = mask.sum()
    if valid == tlength:
        return track

    xs = np.where(mask != 0)[0]
    ys = track.reshape([tlength, -1])[xs, :]
    x = np.arange(tlength)

    # ========================================================================
    # Interpolation.
    # ========================================================================
    xs = xs.astype(ys.dtype)
    x = x.astype(ys.dtype)
    # Pad control points for extrapolation.
    xs = np.concatenate([[np.finfo(xs.dtype).min], xs, [np.finfo(xs.dtype).max]], axis=0)
    ys = np.concatenate([ys[:1], ys, ys[-1:]], axis=0)

    # Compute slopes, pad at the edges to flatten.
    sloops = (ys[1:] - ys[:-1]) / np.expand_dims((xs[1:] - xs[:-1]), axis=-1)
    sloops = np.pad(sloops[:-1], [(1, 1), (0, 0)])

    # Solve for intercepts.
    intercepts = ys - sloops * np.expand_dims(xs, axis=-1)

    # Search for the line parameters at each input data point.
    # Create a grid of the inputs and piece breakpoints for thresholding.
    # Rely on argmax stopping on the first true when there are duplicates,
    # which gives us an index into the parameter vectors.
    idx = np.argmax(np.expand_dims(xs, axis=-2) > np.expand_dims(x, axis=-1), axis=-1)
    sloop = sloops[idx]
    intercept = intercepts[idx]

    # Apply the linear mapping at each input data point.
    y = sloop * np.expand_dims(x, axis=-1) + intercept
    y = y.astype(ys.dtype)
    y = y.reshape(orig_shape)
    return y

【コード解説】
- 引数
  - track: `[T, J, C]` 形状の追跡点配列．欠損値はゼロ埋めされている必要があります．
    また，この関数は部位毎に追跡点配列が入力される (全追跡点，特徴量で欠損フレームが共通) ことを想定しています．
      - T: 動画フレームインデクス
      - J: 追跡点インデクス
      - C: 特徴量インデクス．今回は $(x, y, z, c)$ の4次元特徴量を用いています．
- 2-3行目: 内部処理で用いるため，`track` の形状情報を取得
- 4行目: 第0番目の追跡点の信頼度に基づいて，追跡成功フレームを示す `mask` を生成．
  この関数は全追跡点，特徴量で欠損フレームが共通であることを前提としています．
- 5-7行目: `mask.sum()` で追跡成功フレーム数を取得し，線形補間が必要かを判定
- 9-10行目: 追跡成功フレームのデータ点を取得．
  `xs` は第2節の $t$ に相当し，`ys` は $y$ に相当します．
  `xs` は全追跡点，全特徴量で共通なのでベクトル配列で保持します．
  `ys` は `[T, J*C]` 形状の行列で保持します．
- 11行目: 補間箇所を含む，全フレームのインデクス配列を生成．これは第2節の $\bm{t}^e$ に相当します．
- 16-17行目: 計算処理のために型を `ys` に合わせて変換
- 19-20行目: `xs` と `ys` の先頭と末尾にダミー値を追加．図3で説明した処理に相当します．
- 23-24行目: 直線の傾き行列を算出し，先頭にダミー値を追加．図4，図5，および図6で説明した処理に相当します．
- 27行目: 直線の切片行列を算出．図7で説明した処理に相当します．
- 33-35行目: ルックアップテーブルを作成して，全フレームのインデクスに対する直線パラメータを取得．
  図9と図10で説明した処理に相当します．
  説明のママの実装ではないので，少し対応関係が分かりにくいかもしれません．
  まず，33行目 `np.argmax()` の内側の比較処理で $\bm{t} > \bm{t}^e$ を満たす箇所を示すマスク配列を生成しています．
  やろうとしていることは図9-2.aの説明箇所に相当します．
  `np.argmax()` は最大値を与えるインデクスを所得する関数で，最大値が複数ある場合は先頭のインデクスを取得します．
  この特性を利用して図9-2.bの処理を実装しています．
  34-35行目は，それぞれ $\bm{\alpha_{j}}$と$\bm{\beta_{j}}$ を取得する処理です．
- 38-40行目: 線形補間を実行し，型と形状を入力に合わせて返す

全部位の補間処理

全部位の補間処理は次の関数で実装してます．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def partsbased_interp(trackdata):
    pose = trackdata[:, :33]
    lhand = trackdata[:, 33:33+21]
    rhand = trackdata[:, 33+21:33+21+21]
    face = trackdata[:, 33+21+21:]

    pose = matrix_interp(pose)
    lhand = matrix_interp(lhand)
    rhand = matrix_interp(rhand)
    face = matrix_interp(face)
    return np.concatenate([pose, lhand, rhand, face], axis=1)

【コード解説】
- 引数:
  - trackdata: `[T, J, C]` 形状の追跡点配列．欠損値はゼロ埋めされている必要があります．
    こちらの追跡点には全部位のデータが含まれていることを想定しています．
- 2-5行目: 追跡点を部位毎に分割
- 7-10行目: 部位毎に線形補間を実行
- 11行目: 部位毎の追跡点を結合して返す

補間処理の実行

線形補間に必要な処理が実装できましたので，上でダウンロードしたデータを用いて処理を実行します．

次のコードは先程実装したpartsbased_interpにtrackdataを入力して，補間後の追跡点newtrackを得ています．
その後，参照用の補間後追跡点との誤差を計測しています．

1
2
3

newtrack = partsbased_interp(trackdata)
diff = (reftrack - newtrack).sum()
print(f"Sum of error:{diff}")

print 処理の結果を示します．

Sum of error:-6.935119145623503e-12

指数に示されるとおり，誤差はほぼありませんでした．

3.5 処理時間の計測

最後に，次のコードで処理時間を計測します．

1
2

target_fn = partial(partsbased_interp, trackdata=trackdata)
pmeasure(target_fn)

最初に，partial() でpartsbased_interp() に入力を指定して関数オブジェクトにしています．
次に，上で実装した処理時間計測クラスに関数オブジェクトを渡して処理時間を計測しています．

print処理の結果を示します．

Overall summary: Max 2.83882ms, Min 625.075µs, Mean +/- Std 856.256µs +/- 386.886µs
Top 10 summary: Max 636.292µs, Min 625.075µs, Mean +/- Std 632.565µs +/- 3.05882µs

(他のプロセスの影響が少ない場合は) 線形補間は平均して \(633\) マイクロ秒程度かかることが分かります．
Numpy関数を用いた実装では\(6.87\)ミリ秒程度だったので，10倍ほど高速に処理できていることが分かります．
また，誤差も微小であることが分かります．

今回は線形補間処理をNumpyの行列計算で実装して高速化を行う方法を紹介しましたが，如何でしたでしょうか?
かなり細かく説明したため，記事が長くなってしまいました(^^;)

今回説明した処理方法は，高速に動作し誤差も微小です．
また，この方法はTensorflowやPyTorchなどでも実装可能で，GPUで処理することもできます．

副作用としては，ルックアップテーブルを作成する際に size(xs) * size(x) のマスクを生成するため，メモリ使用量が interp を用いる場合よりも大きい点が挙げられます．
大体のケースでは無視できる範囲ですが，非常に長い系列を入力する場合はご注意ください．

今回紹介した話が，補間処理などでお悩みの方に何か参考になれば幸いです．