3. 多粒子運動計算処理としてのMacaron Net

3.1 Transformer = 1次精度の計算処理
3.2 Macaron Net = 2次精度の計算処理

4. 追加実験
5. 付録: Splitting scheme の検証コード

こんにちは．高山です．
今回の記事は，Macaron Net を用いた孤立手話単語認識 (以降では実験記事と記載します) の補足になります．

以前の記事で Macaron Net [Lu'19] を用いた孤立手話単語認識を紹介しました．
このときは実装と実験結果を中心として説明し，背景となるアイデアや考え方には触れませんでしたので，本記事で補足説明をさせていただきたいと思います．

今回は Macaron Net を理解する上で前提となる考え方から説明しています．
そのため記事が少し長いので，要点を下記に記します．

Neural Network (NN) でよく使われる Residual Connection は "特徴空間の粒子の運動" という物理学のアナロジーで定式化ができる．
この場合，Transformer は "特徴空間における多粒子の運動" としてとらえることができる．
しかし，Transformer は精度の低い計算処理を模したレイヤ構造をしている．
精度の高い計算処理を模したレイヤ構造として，Macaron Net を提案する．

基本的に上記の流れに沿って説明していきます．
数学的に厳密な説明は大変なので (と言うよりも高山の数学力では難しいので(^^;))，概念的な説明になりますのでご了承ください．

[Lu'19]: Y. Lu, et al., "Understanding and Improving Transformer From a Multi-Particle Dynamic System Point of View," arXiv:1906.02762, available here, 2019.

更新履歴 (大きな変更のみ記載しています)

2024/09/17: タグを更新しました

1. Macaron Netについておさらい

まず最初に，Macaron Net [Lu'19] のおさらいをしたいと思います．
図1に，Transformer [Vaswani'17] から Macaron Net への変更点を示します．

図1: Macaron Net のアーキテクチャ — Macaron Net のアーキテクチャ

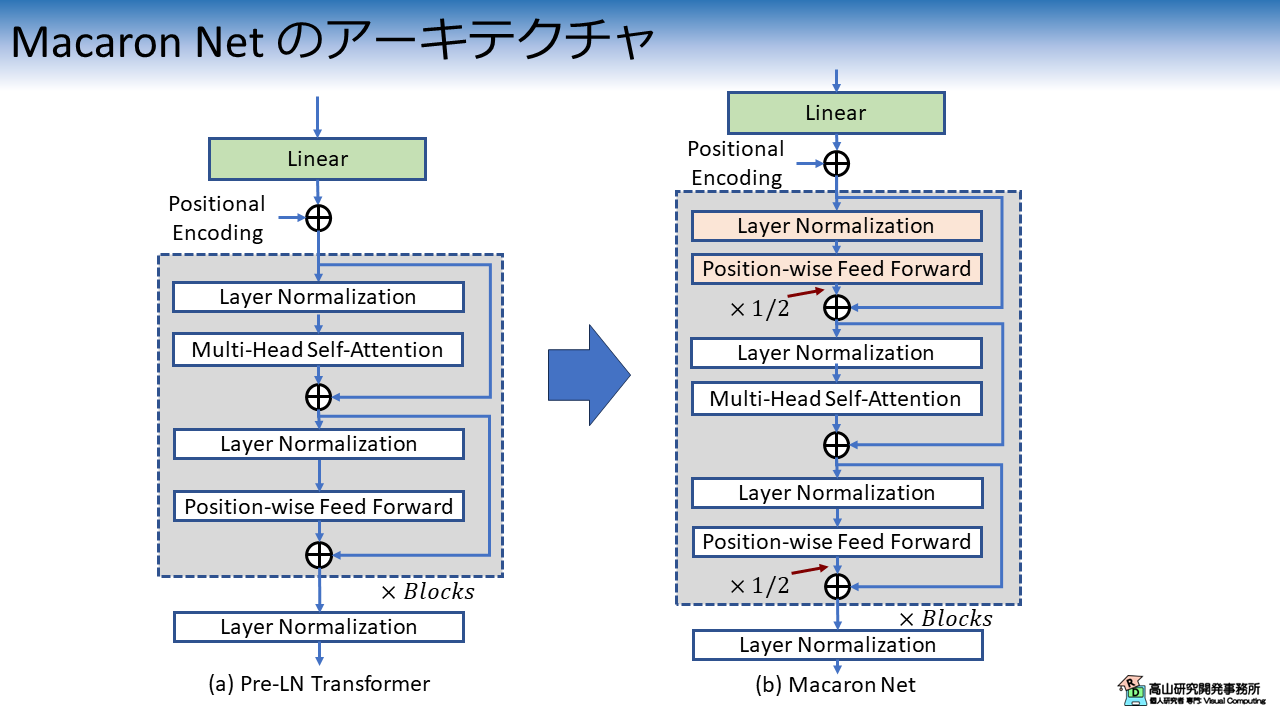
図1(b) に示すように，Macaron Net では Multi-Head Self-Attention (MHSA) 層の前に Position-wise Feed Forward (PFFN) 層を追加します．
さらに，PFFN の Residual Connection (分岐との和) では PFFN の出力に $1/2$ をかけて足し合わせます．

このアーキテクチャの効果は実験記事のとおり (第2.2項をご参照ください) です．
文献[Lu'19] と同様の構成 (Layer Normalizationを使用) を用いた場合は Transformer に対して認識性能が向上していました．

しかしながら，このアーキテクチャはどのような発想で生まれたのでしょうか?
本記事ではこの点をもう少し掘り下げて説明したいと思います．

[Lu'19]: Y. Lu, et al., "Understanding and Improving Transformer From a Multi-Particle Dynamic System Point of View," arXiv:1906.02762, available here, 2019.
[Vaswani'17]: A. Vaswani, et al., "Attention Is All You Need," Proc. of the NIPS, available here, 2017.

2. Macaron NetにおけるNNレイヤの解釈

2.1 特徴量を特徴空間の粒子ととらえる

本節では，Macaron Net のアイデアを理解する上で基本となる考え方を説明したいと思います．

実験記事の冒頭で，文献[Lu'19] では Transformer の処理を "特徴空間内における多粒子の運動現象 (移流拡散現象) と見なす" と書きました．
これだけ聞くと，"多粒子? 物理の話?" と感じるかもれしれませんね．
実際には物理現象そのものを取り扱うわけではありません．

"粒子" や "運動" という用語は，計算処理を物理現象のアナロジーとして捉えるための言い換えで，実際は "特徴量" と "特徴量の変化" を指します．

"特徴量" の中身は多次元の数値データです．
図2に示すように，各数値を多次元空間の座標値とみなすと，1個の特徴量は特徴空間の1点としてとらえることができます．

図2: 特徴量 = 特徴空間の点 = 粒子 — 特徴量 = 特徴空間の点 = 粒子

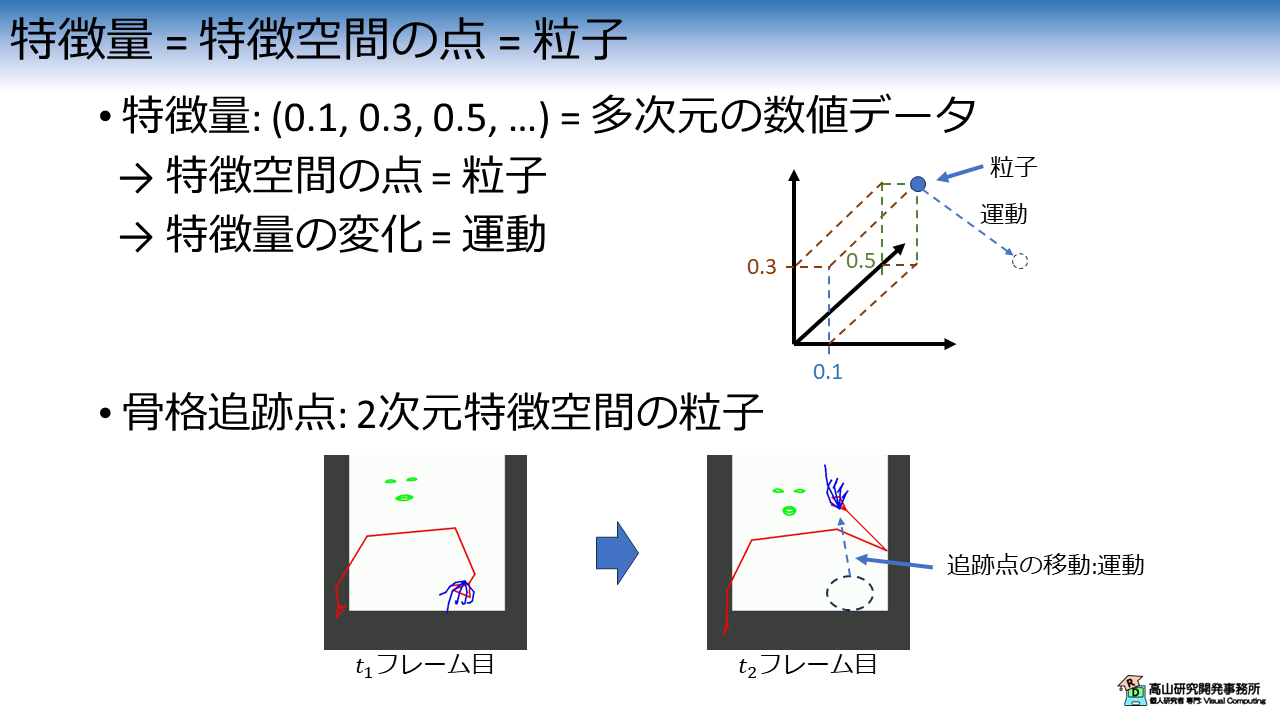
文献[Lu'19] ではこの特徴空間の1点のことを"粒子" と呼び，特徴量の変化を (特徴空間における) "粒子の運動" ととらえます．

今まで手話認識で扱ってきた，骨格追跡点も 2次元特徴空間の粒子とみなすことができます．
この場合は，特徴量が座標そのものなので分かりやすいですね．

[Lu'19]: Y. Lu, et al., "Understanding and Improving Transformer From a Multi-Particle Dynamic System Point of View," arXiv:1906.02762, available here, 2019.

2.2 常微分方程式と Residual Connection

常微分方程式

ここで少しだけ物理・数学の話をさせてください．
粒子の運動のような時間的な変化は，下記に記すような常微分方程式で表されることが多いです．

$$ \frac{dx}{dt} = f(x,t); f(x, 0) = x_0 $$

$x_0$ は求めたい変数の初期値で，$dx/dt$ は時間 $t$ の変化に対する変数 $x$ の変化量を示します．
式で書くと何か難しそうに見えますが，"最初の値 ($x_0$) と各時間の変化量 ($dx/dt$) が分かれば，変数 $x$ が予測できる" と言っているだけです．

上記の方程式は数式的な操作で解く ($x=\bigcirc \bigcirc$ を導き出すことです．解析的に解くと言ったりします) ことができない場合が多いです．
このような場合は，次式のように微分 ($dx, dt$) を離散的な時間ステップにおける変化で置き換えて，順次計算を行えるようにします．
(このような変換を経て数値を求める方法はオイラー法と呼ばれます)

$$ \frac{x_{t+\Delta t} - x_t}{\Delta t} = f(x, t) $$

$\Delta t = 1$ とすると，次式のようになります．

\begin{equation} x_{t+1} - x_t = f(x, t) \label{eqn:diff_ode} \end{equation}

大分簡単になりましたね．
微分方程式を見ると (高山のように(^^;)) 拒否反応が出る方もいらっしゃるかもしれませんが，実装上はかなりシンプルであったり普段から行っていることであったりします．

Residual Connection の解釈

式($\ref{eqn:diff_ode}$) によく似た形式の計算は，Residual Connection [He'15] と呼ばれる NN 構造に出てきます．
Residual Connection と，その数式表現を図3に示します．

図3: Residual Connection と常微分方程式 — Residual Connection と常微分方程式

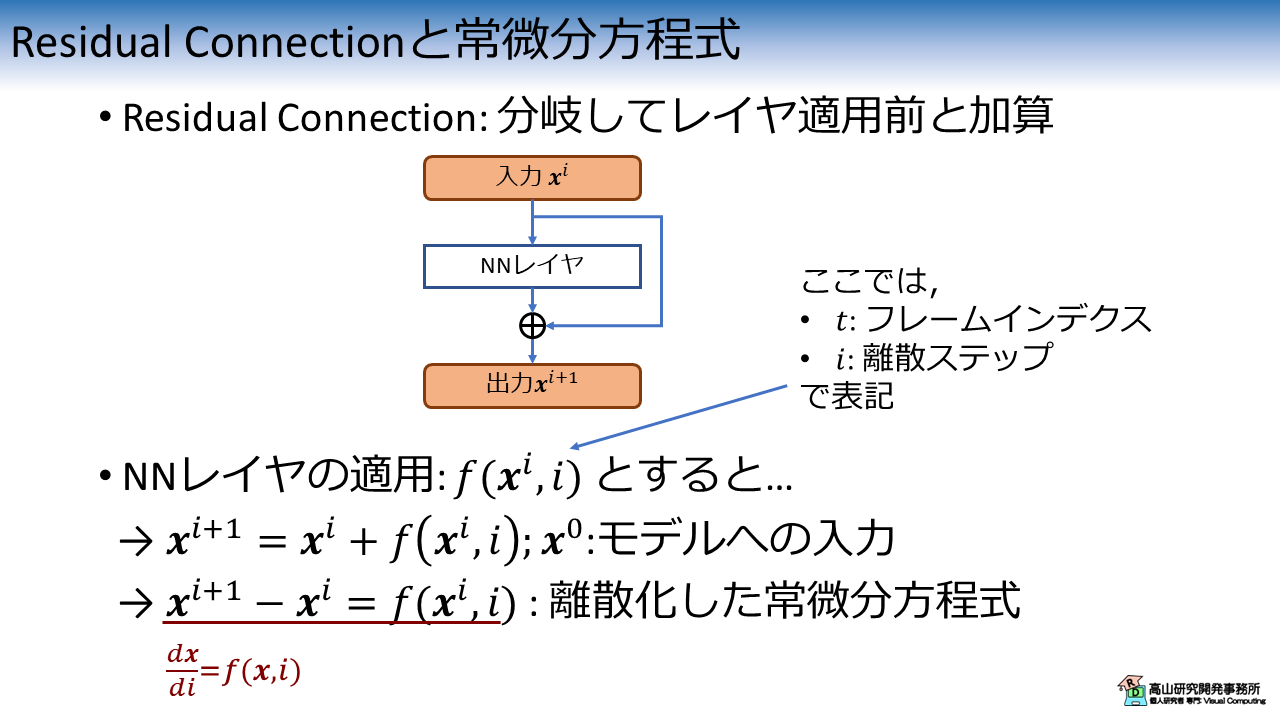
Residual Connection を持つ NN レイヤでは，レイヤ適用前後の特徴量を足し合わせて出力します．
数式で表すと次式のようになります．

$$ \boldsymbol{x}^{i+1} = \boldsymbol{x}^i + f(\boldsymbol{x}^i, i) $$

$\boldsymbol{x}^i$ は $i$ 番目の NNレイヤへの入力で，$\boldsymbol{x}^0$ はモデルへの入力を示します．
$\boldsymbol{x}^i$ を左辺へ移項すると，次式のようになります．

\begin{equation} \boldsymbol{x}^{i+1} - \boldsymbol{x}^i = f(\boldsymbol{x}^i, i) \label{eqn:diff_resnet} \end{equation}

式($\ref{eqn:diff_ode}$) と式($\ref{eqn:diff_resnet}$) は (添字以外は) 同じ数式表現になっています．
NN では特徴量はレイヤが進む毎に変化していくので，変化軸の離散ステップは $i$ で示しています．
$t$ は時系列のフレームインデクスを示すために以降の節で使用します．

第2.1項で "特徴量は特徴空間の粒子として表せる" と言ったのを覚えていますか?
Residual Connection を用いた NNレイヤの計算処理が "特徴空間における粒子の運動を示す" という表現は，式($\ref{eqn:diff_ode}$) と式($\ref{eqn:diff_resnet}$) のアナロジーから来ています．

なお，Residual Connection を常微分方程式の数値解法としてとらえるアイデアは，文献[Lu'19] 以前から提案されています [Lu'17, Haber'17, Chen'18, Ruthotto'20] ([Ruthotto'20]の初出は2018年です)．
特に Neural ODE [Chen'18] は有名な論文ですのでご興味があれば読んでみてください (Macaron Net との関係は薄いですが)．

[He'15]: K. He, et al., "Deep Residual Learning for Image Recognition," Proc. of the CVPR, available here, 2015.
[Lu'19]: Y. Lu, et al., "Understanding and Improving Transformer From a Multi-Particle Dynamic System Point of View," arXiv:1906.02762, available here, 2019.
[Lu'17]: Y. Lu, et al., "Beyond Finite Layer Neural Networks: Bridging Deep Architectures and Numerical Differential Equations," Proc. of the ICML, available here, 2017.
[Haber'17]: E. Haber, et al., "Stable Architectures for Deep Neural Networks," Inverse Problems, Vol.34, No.1, available here, 2017.
[Chen'18]: R. T. Q. Chen, et al., "Neural Ordinary Differential Equations," Proc. of the NIPS, available here, 2018.
[Ruthotto'20]: L. Ruthotto, et al., "Deep Neural Networks Motivated by Partial Differential Equations," J. Math. Img. Vis., Vol.62, pp:352-364, available here, 2020.

2.3 Macaron Net の考え方

ここまでの説明を踏まえて，文献[Lu'19]の主張を図4に示します．

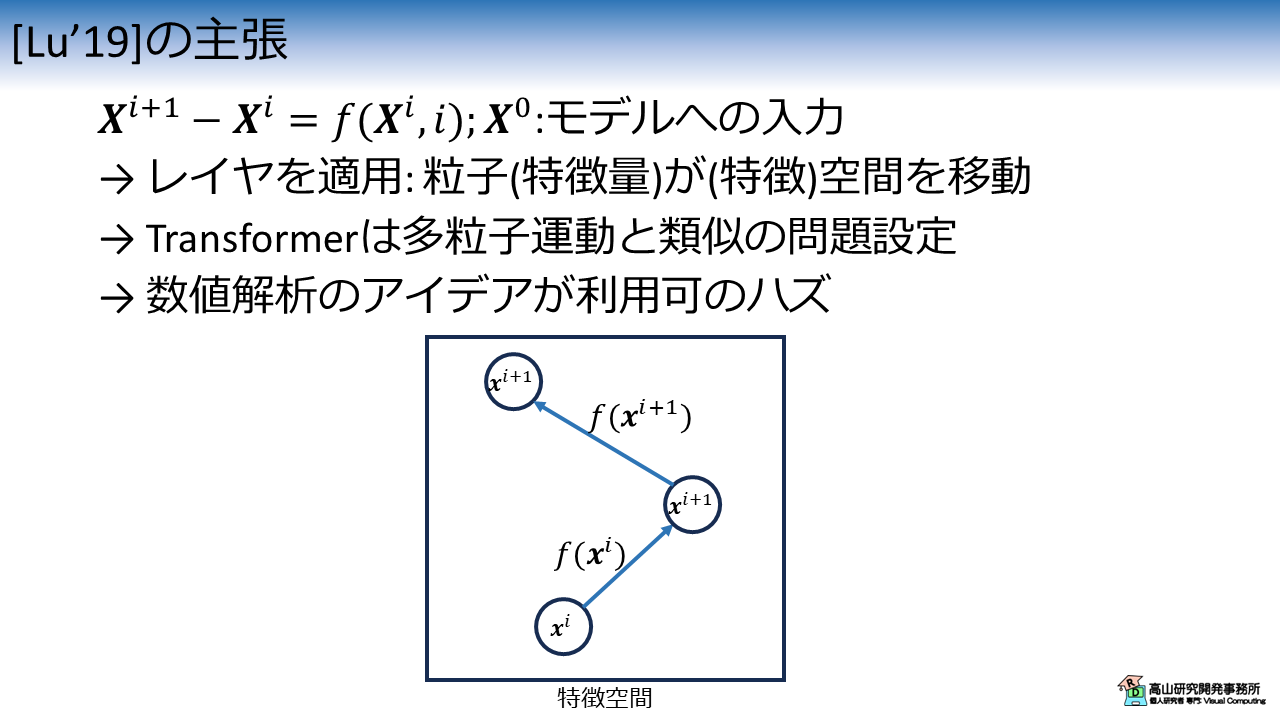
第2.2項で説明したとおり， Residual Connection を用いた NNレイヤの計算処理は特徴空間における粒子の運動を示します．
Transformer では時系列データを扱うため，各フレームを1個の粒子と考えると，特徴空間における多粒子運動の問題とみなせます．

多粒子運動の問題は数値解析の分野で古くから取り組まれており，近似解を得る手法が提案されています．
第3節では， Transformer や Macaron Net が数値解析分野の手法と類似の処理構造を持っていることを見ていきます．

[Lu'19]: Y. Lu, et al., "Understanding and Improving Transformer From a Multi-Particle Dynamic System Point of View," arXiv:1906.02762, available here, 2019.

3. 多粒子運動計算処理としてのMacaron Net

3.1 Transformer = 1次精度の計算処理

図5に Transformer [Vaswani'17] の処理ブロックを示します．

図5: Transformer = Lie-Trotter splitting scheme — Transformer = Lie-Trotter splitting scheme

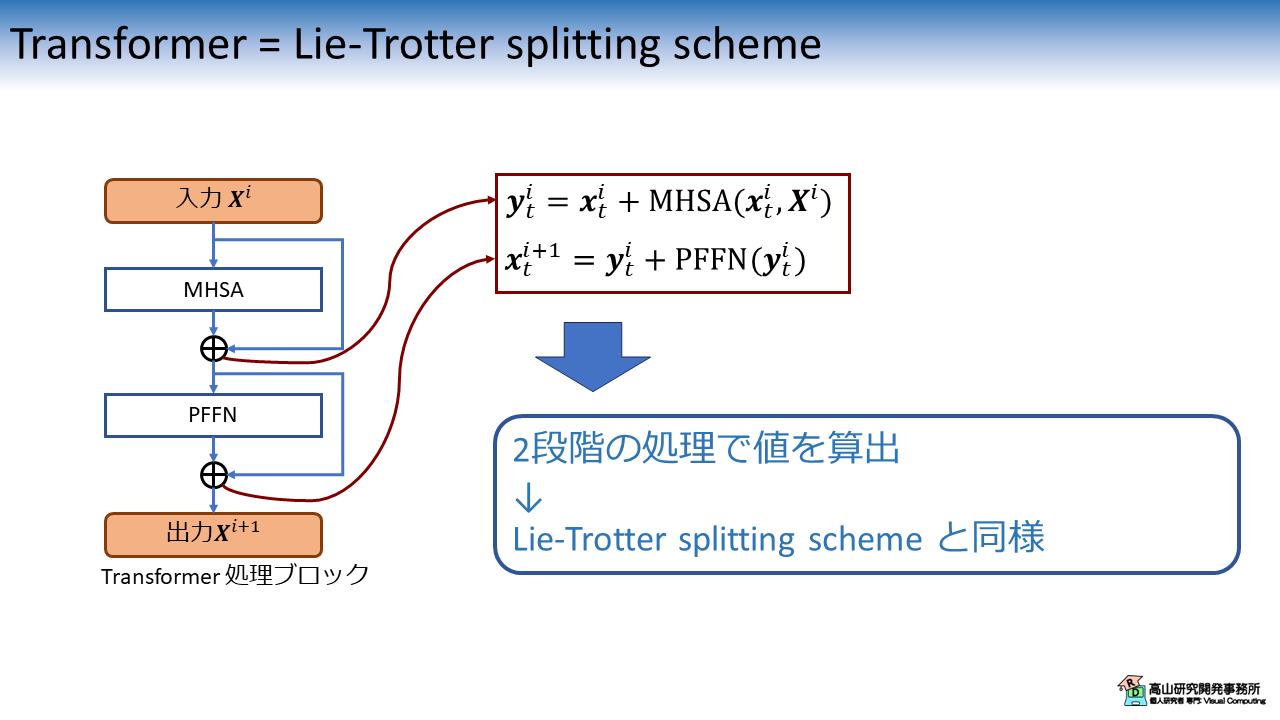
オリジナルの Transformer では，入力 $\boldsymbol{X}^i$ に対して MHSA と PFFN を順次適用して出力 $\boldsymbol{X}^{i+1}$ を得ます．
数式で表すと下記のようになります．

\begin{eqnarray} \boldsymbol{y}^i_{t} & = & \boldsymbol{x}^i_t + MHSA(\boldsymbol{x}^i_t, \boldsymbol{X}^i), \nonumber \\ \boldsymbol{x}^{i+1}_t & = & \boldsymbol{y}^i_t + PFFN (\boldsymbol{y}^i_t) \label{eqn:transformer} \end{eqnarray}

2段階の計算処理を経て値を算出していることが分かります．
この処理構造が数値解析分野における Lie-Trotter splitting scheme と同様であることが，文献[Lu'19] では主張されています．
(Lie-Trotter splitting scheme の原著は見つけられませんでした．これかな...? というものはあったのですが高山の数学力不足から確信が持てませんでした...)

Lie-Trotter splitting scheme

Lie-Trotter splitting scheme の概要を図6に示します．

Lie-Trotter splitting scheme は，

\begin{eqnarray} \frac{dx}{di} & = & f_1(x, i) + f_2(x, i), \nonumber \\ \rightarrow \frac{x^{i + \Delta i} - x^i}{\Delta i} & = & f_1(x^i, i) + f_2(x^i, i) \nonumber \end{eqnarray}

のような形式の常微分方程式に対して，

\begin{eqnarray} y^i & = & x^i + \Delta i f_1(x^i, i), \nonumber \\ x^{i+1} & = & y^i + \Delta i f_2(y^i, i) \nonumber \end{eqnarray}

というステップで近似解を得る手法です．

文献[Lu'19] の表記を借りて多粒子の運動を次のように表します．

$$ \frac{d\boldsymbol{x}^i_t}{di} = F(\boldsymbol{x}^i_t, \boldsymbol{X}^i) + G(\boldsymbol{x}^i_t) $$

この式は，Lie-Trotter splitting scheme を用いて次のように分解することができます．

\begin{eqnarray} \boldsymbol{y}^i_t & = & \boldsymbol{x}^i_t + \Delta i F(\boldsymbol{x}^i_t, \boldsymbol{X}^i) \nonumber \\ \boldsymbol{x}^{i+\Delta i} & = & \boldsymbol{y}^i_t + \Delta i G(\boldsymbol{y}^i_t) \label{eqn:lt_split} \end{eqnarray}

式(\ref{eqn:lt_split}) は先程示した Transformer の数式表現である式(\ref{eqn:transformer}) と対応関係にあることが分かります．

余談

文献[Lu'19] では，$F(\cdot)$ を拡散項 (diffusion term)，$G(\cdot)$ を移流項 (convection term) と呼んでおり， Transformer の処理は移流拡散方程式 (Convection-Diffusion equation) の計算処理であると述べています．
(実際にはソルバであると書いてますが，計算処理でも良いかなと思いこのような表記にしています)

"移流"や"拡散"は物理学の用語です．
調べると難しい数式が山ほど出てきて正直ビビリます (^^;)．

文献[Lu'19] ではこれらの用語に対して細かな言及はなく，

移流運動: 粒子毎に独立に計算する処理
拡散運動: 粒子間の影響を計算する処理

ということがサラッと書いてあります．

ニュアンスは分かるのですが，用語の使い方が適切なのか (数学的に正確に対応しているのか) どうかは未だに確信が持てていません．
(なお，こういった細かいところを気にして物理や数値解析の文献を追っていくと，(高山のように) 深みにハマります (^^;) ので注意してください．読むこと自体は面白いですが)

[Vaswani'17]: A. Vaswani, et al., "Attention Is All You Need," Proc. of the NIPS, available here, 2017.
[Lu'19]: Y. Lu, et al., "Understanding and Improving Transformer From a Multi-Particle Dynamic System Point of View," arXiv:1906.02762, available here, 2019.

3.2 Macaron Net = 2次精度の計算処理

Lie-Trotter splitting scheme は 1次精度 (近似精度の低い) 手法であることが知られています．
では，より近似精度の高い手法を用いれば性能があがるのでは? という発想が自然に出てくると思います．

Macaron Net は Strang-Marchuk splitting scheme [Strang'68] という 2次精度の計算手法を基にレイヤ構造を設計しています．
Strang-Marchuk splitting scheme と Macaron Net の関係を図7に示します．

図7: Strang-Marchuk splitting scheme と Macaron Net — Strang-Marchuk splitting scheme と Macaron Net

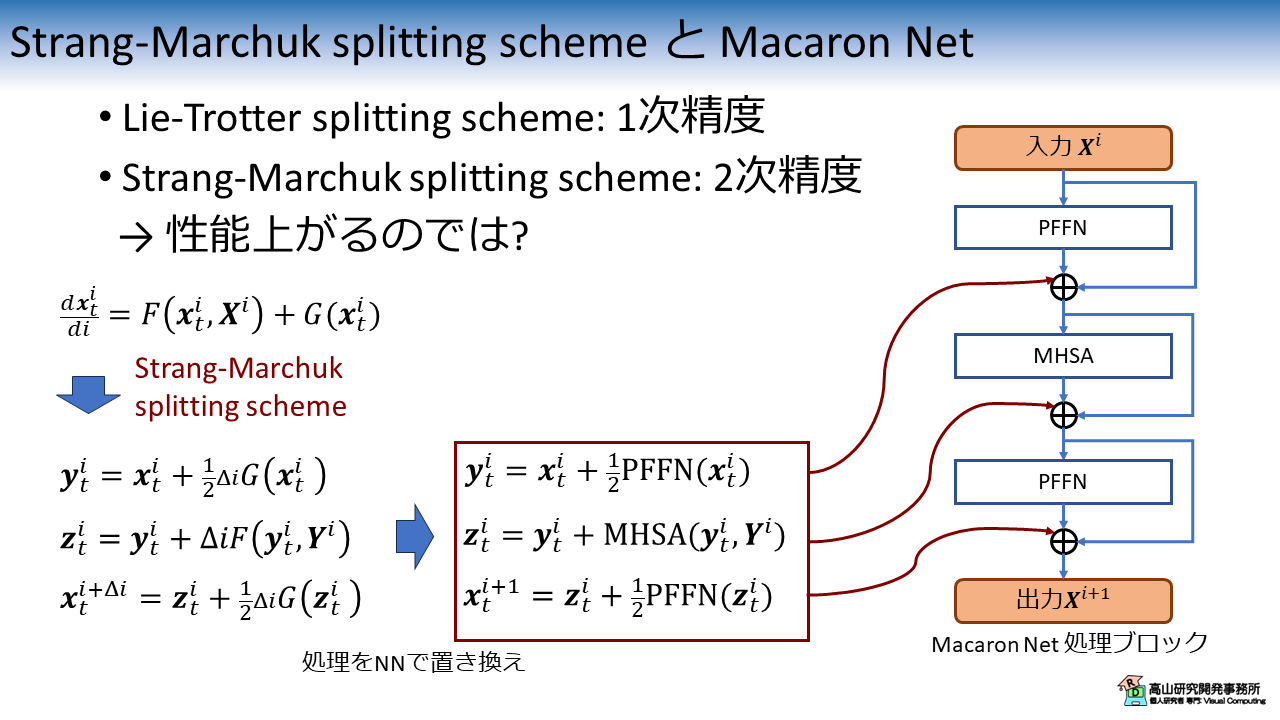
Strang-Marchuk splitting scheme では，多粒子の運動は下記に示す計算処理に分解されます．

\begin{eqnarray} \boldsymbol{y}^i_t & = & \boldsymbol{x}^i_t + \frac{1}{2} \Delta i G(\boldsymbol{x}^i_t), \nonumber \\ \boldsymbol{z}^i_t & = & \boldsymbol{y}^i_t + \Delta i F(\boldsymbol{y}^i_t, \boldsymbol{Y}^i), \nonumber \\ \boldsymbol{x}^{i+\Delta i}_t & = & \boldsymbol{z}^i_t + \frac{1}{2} \Delta i G(\boldsymbol{z}^i_t) \label{eqn:sm_split} \end{eqnarray}

図6に示すとおり，式(\ref{eqn:sm_split}) は Macaron Net の計算処理と対応関係にあります．

このレイヤ構造の効果は実験記事のとおり (第2.2項をご参照ください) で，文献[Lu'19] と同様の構成 (Layer Normalizationを使用) を用いた場合は Transformer に対して認識性能が向上していました．

[Strang'68]: G. Strang, "On the Construction and Comparison of Difference Schemes," SIAM J. Numer. Anal., Vol.5, No.3, 1968

4. 追加実験

今回の記事を書いている途中で，Macaron Net の実装について下記のような疑問を持ちました．

PFFN ブロックの Residual Connection でかける係数 $1/2$ は必要か．
1番目と2番目の PFFN レイヤは同一の重みでなくてよいのか．

まず1番目の疑問に関してですが，数値解析の場合と違い PFFNレイヤの関数は学習によって決まります．
そのため，$1/2$ のようなスカラー倍の係数は学習によって NN層の重みで調整されるのでは?，と思いました．

2番目の疑問に関しては，Macaron Net では 1番目と 2番目の PFFN レイヤをそれぞれ個別にインスタンス化して実装しています．
この場合，それぞれのレイヤは異なる重みを持つため，厳密には Strang-Marchuk splitting scheme と異なる処理になるのでは?，と感じました．

上記の疑問を解消するために追加の実験を行いました．
結果を図8に示します．

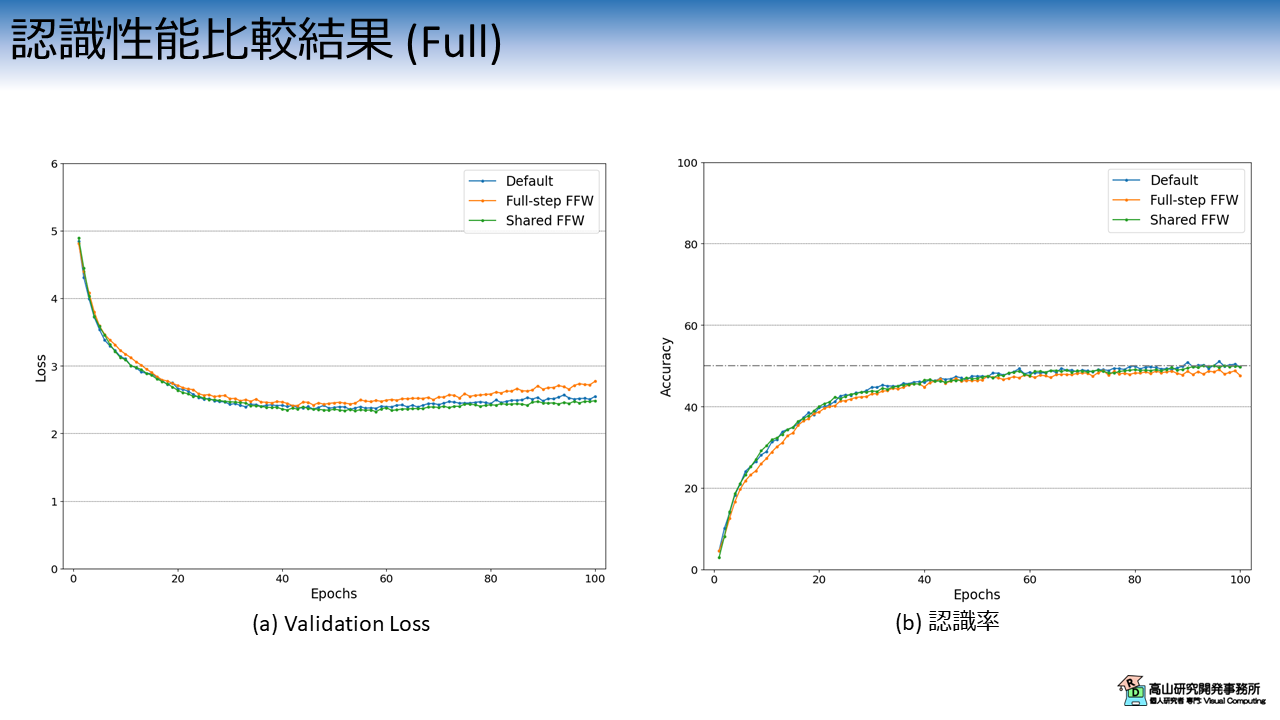
横軸は学習・評価ループの繰り返し数 (Epoch) を示します．
縦軸は実験条件毎の (a) Validation Loss と (b) 認識率の推移を示しています．

各線の色と実験条件の関係は次のとおりです．

青線 (Default): 実験記事における "Macaron-Net-L" と同条件
橙線 (Full-step FFW): PFFN ブロックにおける Residual Connection の係数を $1$ に変更
緑線 (Shared FFW): 1番目と 2番目のPFFN 層の重みを共有

橙線の結果の結果を見ると，学習初期と後半で他の条件よりも結果が悪くなっています．
Residual Connection の係数を $1$ に変更することは悪影響がありそうです．
よくよく考えてみると，学習初期で係数差による誤差が大きく出てしまうと，その後の結果に影響が出るのではと感じました．

重みを共有した場合で性能にほとんど差がないのは意外でした (ロスに関しては若干良くなっているように見えます)．
細かな解析はまだできていませんが，1番目と 2番目の PFFN層は似たような重みを持つ傾向があるのかもしれません．

冗長な PFFN層をまとめたり，Neural ODE のようにループ処理で任意の深さの Macaron Net ができるかもしれないなと感じました．

5. 付録: Splitting scheme の検証コード

最後に，解析解が求まる関数で Splitting scheme の挙動を検証してみましたので，付録として添付します．
なお，下記のコードはH. P. Langtangen氏と S. Linge氏のWeb書籍 (CC-4.0 Attribution で配布されています) を参考にしました．

下記のコードでは初期値 $0.1$ のロジスティック方程式を各手法で近似しています．
この条件の場合，微分方程式は $x(t) = (9e^{-t}+1)^{-1}$ と解けるので，理想値との誤差を確認することが可能です．
Colab上で動作するはずですので，ご興味があれば試してみてください．

# Import modules.
import numpy as np
import matplotlib.pyplot as plt

# =========================================================================
# Define functions.
# =========================================================================
# Logistic equation.
def scaled_logistic(steps, initial, growth_rate=1.0, capacity=1.0):
  coef = capacity / initial -1
  values = [capacity / (1 + coef * np.exp(-growth_rate * t)) for t in steps]
  return values


# Forward euler.
def forward_euler(steps, initial, dt):
  values = [initial]
  for _ in range(len(steps)-1):
    prev = values[-1]
    next = prev + dt * (prev - prev ** 2)
    values.append(next)
  return values


# Lie-Trotter.
def lt_split(steps, initial, dt):
  values = [initial]
  for _ in range(len(steps)-1):
    prev = values[-1]
    temp = prev + dt * prev
    next = temp + dt * (-temp ** 2)
    values.append(next)
  return values


# Strang-Marchuk.
def sm_split(steps, initial, dt):
  values = [initial]
  for _ in range(len(steps)-1):
    prev = values[-1]
    temp0 = prev + dt/2 * prev
    temp1 = temp0 + dt * (-temp0 ** 2)
    next = temp1 + dt/2 * temp1
    values.append(next)
  return values

# =========================================================================
# Calculate and plot results.
# =========================================================================
# Condition.
initial = 0.1
dt = 0.5
t_start = 0
t_end = 10
steps = np.arange(t_start, t_end, dt)

# Calculate.
values_exact = scaled_logistic(steps, initial)
values_nosplit = forward_euler(steps, initial, dt)
values_lt = lt_split(steps, initial, dt)
values_sm = sm_split(steps, initial, dt)

# Plot result.
plt.figure()
plt.plot(steps, values_exact, label="Exact")
plt.plot(steps, values_nosplit, label="No split", linestyle="dashed")
plt.plot(steps, values_lt, label="Lie-Trotter", linestyle="dotted")
plt.plot(steps, values_sm, label="Strang-Marchuk", linestyle="dashdot")
plt.xlim(0, 10)
plt.ylim(0, 1.0)
plt.legend()
plt.show()

今回は Macaron Net のアイデアや考え方について説明しましたが，如何でしたでしょうか?
もう少しスマートに説明したかったのですが，私の物理，数学理解力不足からざっくりとした説明しかできませんでしたね...

ただ，Macaron Net や Neural ODE の考え方はかなり興味深いです．
ちゃんと理解することができれば，色々と新しい発想が生まれそうな気がしますので，引き続き追っていこうと思います．

今回紹介した話が，これから深層学習を勉強してみようとお考えの方に何か参考になれば幸いです．

実践手話認識 - モデル開発編補足: Macaron Netのアイデアについて

This image is generated with ChatGPT-4 Omni, and edited by the author.

作成日: 2024年08月26日(月) 00:00

最終更新日: 2024年09月18日(水) 09:47

カテゴリ: 手話言語処理

タグ: 実践手話認識 Macaron Net 深層学習

更新履歴 (大きな変更のみ記載しています)

1. Macaron Netについておさらい

2. Macaron NetにおけるNNレイヤの解釈

2.1 特徴量を特徴空間の粒子ととらえる