3. 追跡点配列への適用例

こんにちは．高山です．
突然ですが，アフィン変換という処理を聞いたことはありますか?
点や図形を移動したり変形したりする操作で，コンピュータビジョンやコンピュータグラフィックスの分野で広く用いられています．
特に動作認識の分野では，画像や追跡点を変形することで学習データを人工的に増やす，データ拡張として用いられることが多いです．
そこで今回は，アフィン変換による骨格追跡点の変形方法を紹介したいと思います．

更新履歴 (大きな変更のみ記載しています)

2024/09/17: タイトル，タグ，サマリを更新しました

1. アフィン変換とは?

アフィン変換とは，図1に示すような平行移動と3種類の線型変換 (拡大縮小，回転，せん断) の組み合わせから成る演算を指します．

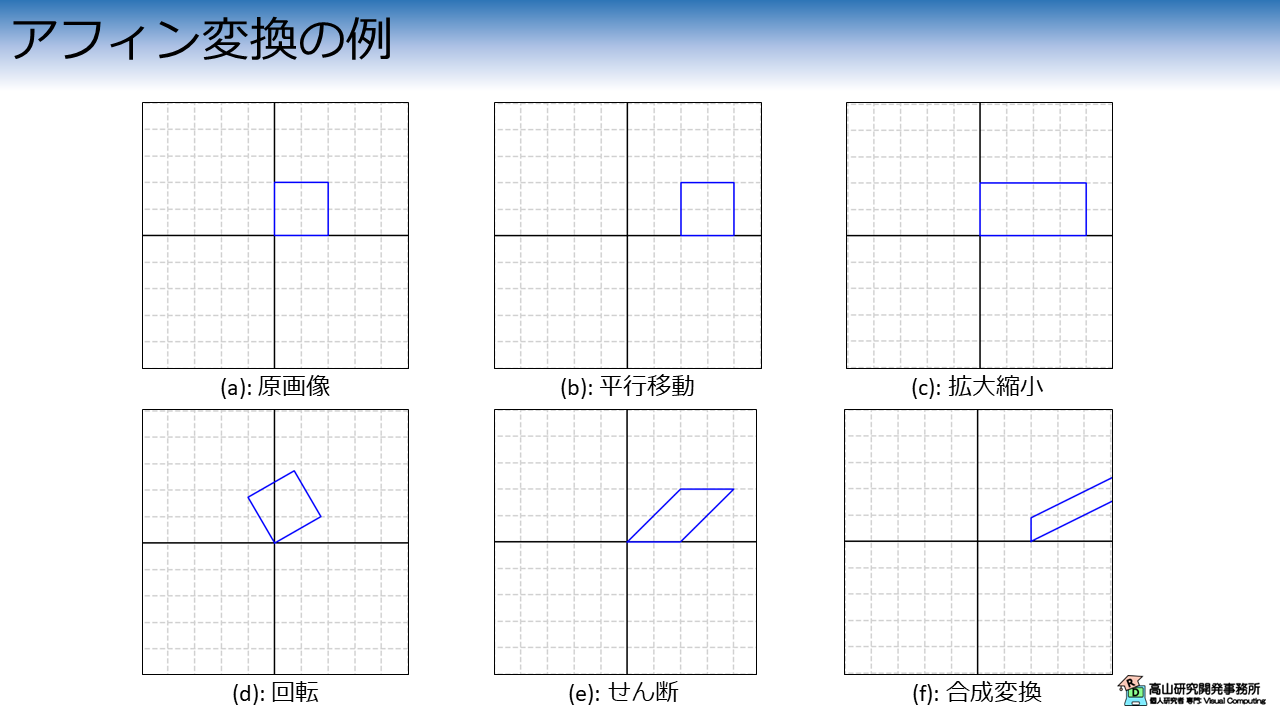
単純な四角形に対してアフィン変換を適用した例を示しています．画像前後の文章で内容を説明しています． — アフィン変換の例

平行移動，拡大縮小，および回転は見たままですが，せん断はイメージしづらいかもしれません．
この処理はある軸の座標値 (例えば$x$) に応じて別の軸の座標値 (例えば$y$) をずらす操作で，矩形は平行四辺形に変換されます．

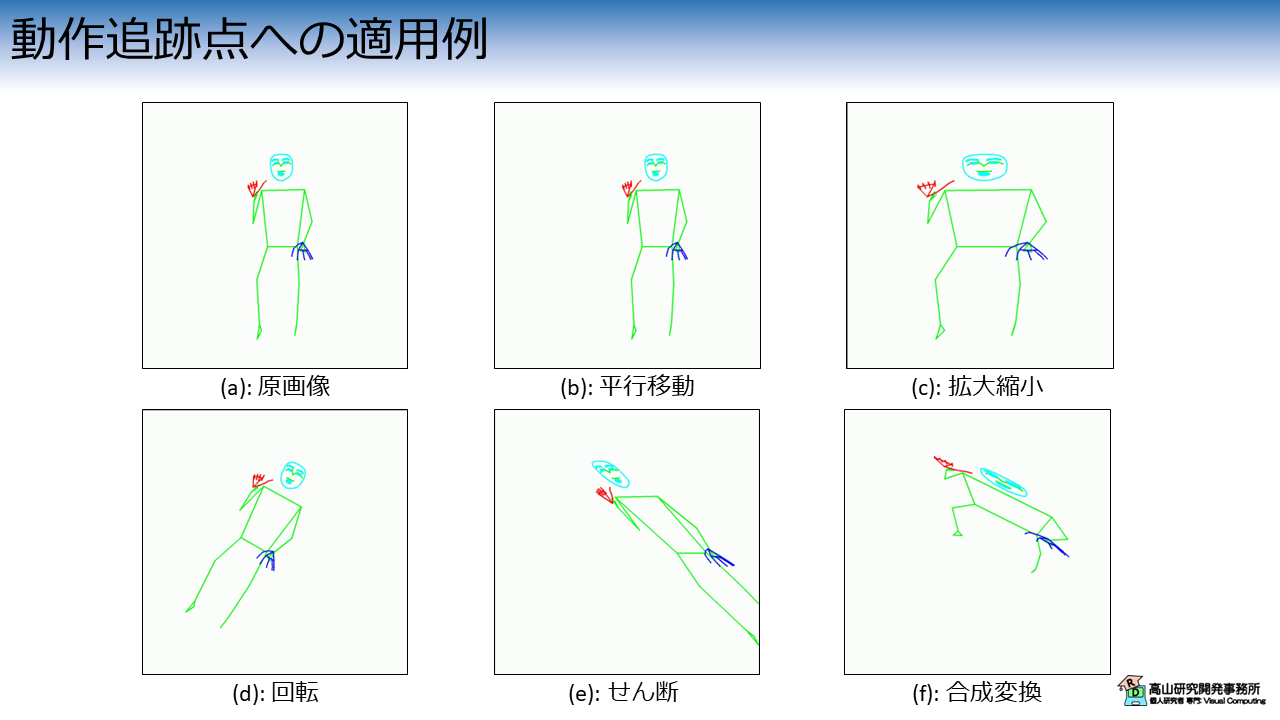
アフィン変換を骨格追跡点に対して適用すると，図2に示すように様々なデータを人工的に作り出すことができます．
図2(a) はMediaPipeの全身追跡の記事で作成したデータを用いて描画しています．
図2は図1と同じ変換方法を使っていますが，変換のされ方が少し違っています．
これは，図2では変換の軸を首周辺に設定していることと，描画に用いたOpenCV (とMediaPipe) では原点が左上にありY軸が下向きになっているためです．
(データを描画してから気づいたのでそのまま使用しています(^^;))

骨格追跡点に対してアフィン変換を適用した例を示しています．画像前後の文章で内容を説明しています． — 骨格追跡点への適用例

アフィン変換は実装も簡単で，変換の組み合わせと変換パラメータ次第で無数のデータが作成できます．
この特徴から，アフィン変換は機械学習時のデータ拡張で用いる標準的な手法の一つになっています．

2. 2次元空間上のアフィン変換

2.1 数式表現

この節では，アフィン変換について簡単な数式を用いて説明していきます．

$X, Y$座標の変換前後の値を，それぞれベクトル $\boldsymbol{P}=(x\ y)^{\mathbb{T}}, \boldsymbol{P'}=(x'\ y')^{\mathbb{T}}$ で表すことにします．
$\mathbb{T}$は転置を示しています．
このとき，アフィン変換は下記のように表すことができます．

$$ \begin{eqnarray} \boldsymbol{P'} & = & \boldsymbol{A}\boldsymbol{P} + \boldsymbol{b} \nonumber \\ \label{eqn_affine_general} \begin{pmatrix} x' \\ y' \end{pmatrix} & = & \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} e \\ f \end{pmatrix} \end{eqnarray} $$

式$\eqref{eqn_affine_general}$の$\boldsymbol{A}$は線型変換 (拡大，縮小，せん断) を示す $2 \times 2$ の行列で，$\boldsymbol{b}$ は平行移動を示すベクトルです．
拡大行列 (Augmented matrix) と拡大ベクトルを用いると，式$\eqref{eqn_affine_general}$は次のように書き換えることができます．

$$ \begin{eqnarray} \begin{pmatrix} \boldsymbol{P} \\ 1 \end{pmatrix} & = & \left ( \begin{array}{c|c} \boldsymbol{A} & \boldsymbol{b} \\ 0\ 0 & 1 \end{array} \right ) \begin{pmatrix} \boldsymbol{P} \\ 1 \end{pmatrix} \nonumber \\ \label{eqn_affine_homo} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} & = & \begin{pmatrix} a & b & e \\ c & d & f \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{eqnarray} $$

式\eqref{eqn_affine_homo} 右辺の行列部分はアフィン変換行列と呼びます．
また，$(x, y, 1)$ のように，拡張した座標を同次座標と呼びます．
(斉次座標 (せいじざひょう) とも呼びます．さいじと呼んで私のように恥かしい思いをしないようにしましょう(^^;)．英語では homogeneous coordinateです)
同次座標を用いることで，線型変換と平行移動を行列の積として統一的に扱うことができます．
こちらの方が便利なのでコンピュータビジョンやコンピュータグラフィックスの分野では専ら式\eqref{eqn_affine_homo}の形式が用いられます．

余談ですが，同次座標を考案したのはメビウスの輪で有名なアウグスト・フェルディナント・メビウスです．
同次座標の名前の由来が知りたくて原著を読もうとしたのですが，ドイツ語で書かれているようで断念しました(^^;)．
一応，同次座標を使うと式\eqref{eqn_affine_homo} (他には同次座標の直線方程式など) が数学用語で言うところの同次性 (homogeneity) を満たすのでこの名前が付いているのかな，と思っています．
もし原著や由来に詳しい方がいらっしゃれば教えていただけるとありがたいです．

2.2 各変換のアフィン変換行列

各変換のアフィン変換行列を下記に記します．

平行移動

$X$軸方向に$t_x$, $Y$軸方向に$t_y$だけ移動するアフィン変換は次の式で表されます．

$$ \begin{equation} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{equation} $$

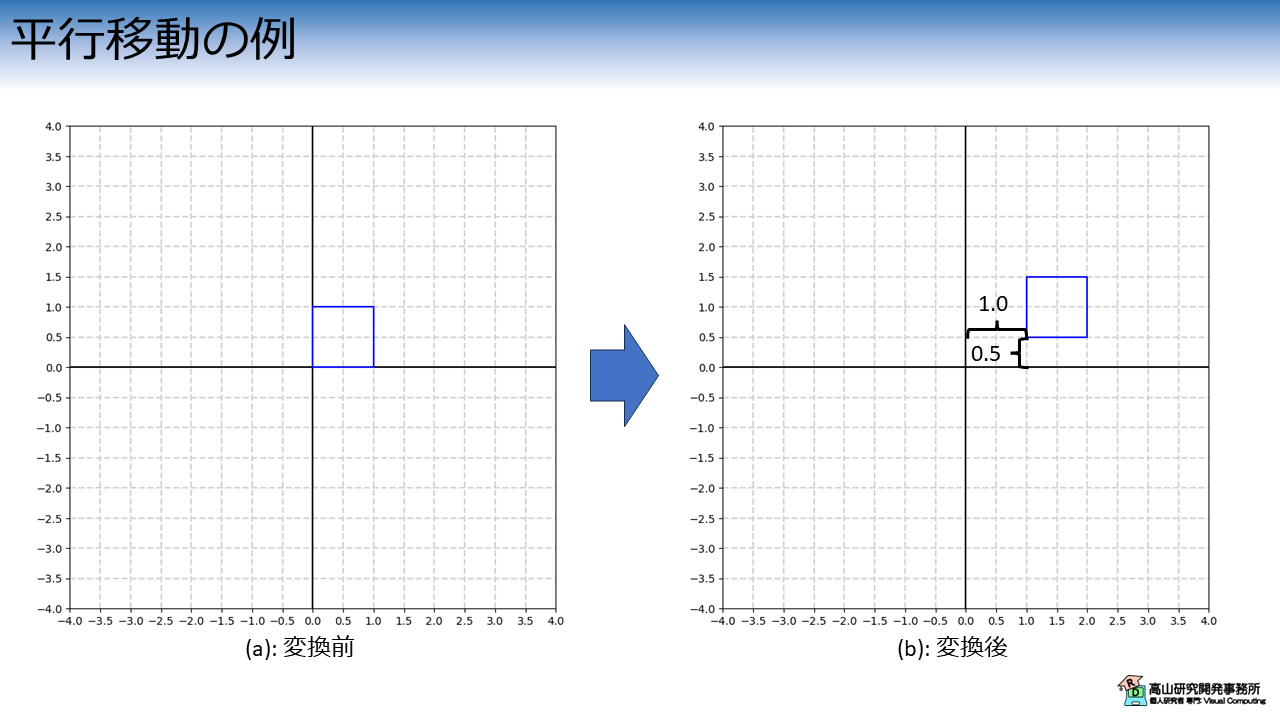
図3は$X$軸方向に$t_x=1.0$, $Y$軸方向に$t_y=0.5$移動するアフィン変換を適用した例です．
変換式は次の式で表されます．

$$ \begin{equation} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 1.0 \\ 0 & 1 & 0.5 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{equation} $$

単純な四角形に対して平行移動を適用した例を示しています．画像直前の文章で処理内容を説明しています． — 平行移動の例

拡大縮小

$X$軸方向に$s_x$, $Y$軸方向に$s_y$だけ拡大縮小するアフィン変換は次の式で表されます．

$$ \begin{equation} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{equation} $$

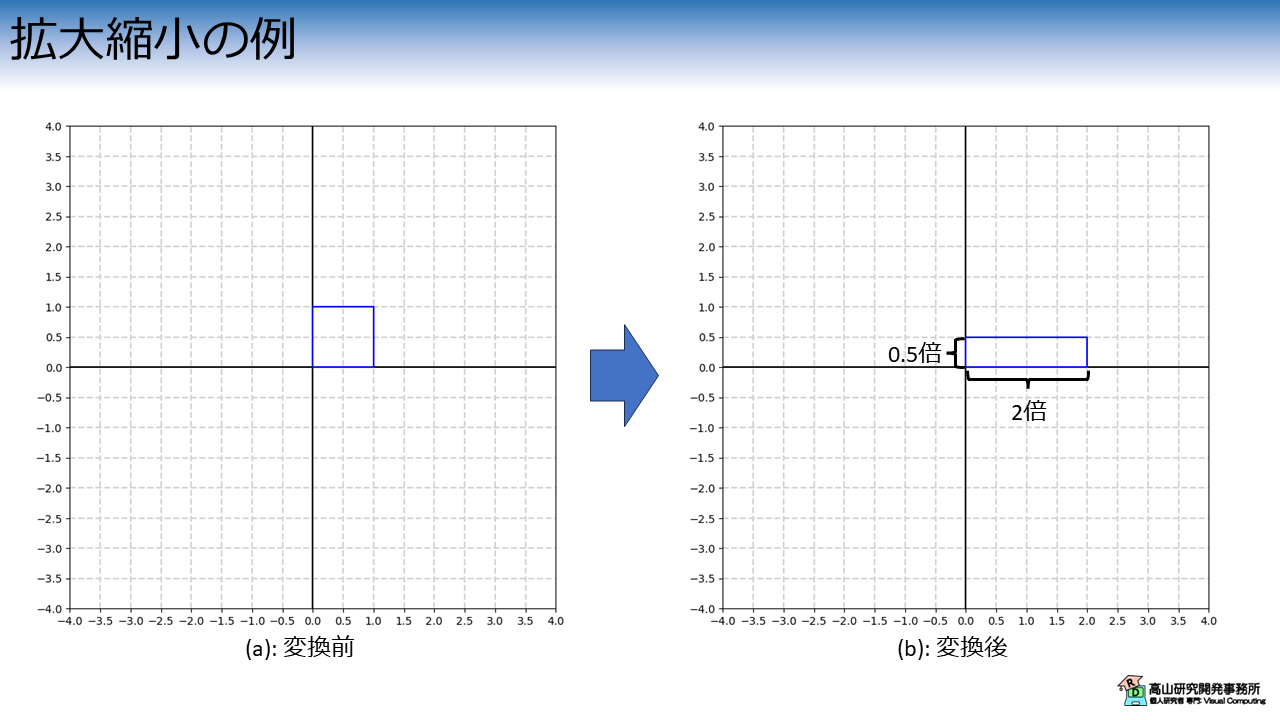
図4は$X$軸方向に$s_x=2.0$, $Y$軸方向に$s_y=0.5$拡大するアフィン変換を適用した例です．
変換式は次の式で表されます．

$$ \begin{equation} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} 2.0 & 0 & 0 \\ 0 & 0.5 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{equation} $$

単純な四角形に対して拡大縮小を適用した例を示しています．画像直前の文章で処理内容を説明しています． — 拡大縮小の例

回転

反時計回りに$\theta$だけ回転するアフィン変換は次の式で表されます．

$$ \begin{equation} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} \cos (\theta) & -\sin (\theta) & 0 \\ \sin (\theta) & \cos (\theta) & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{equation} $$

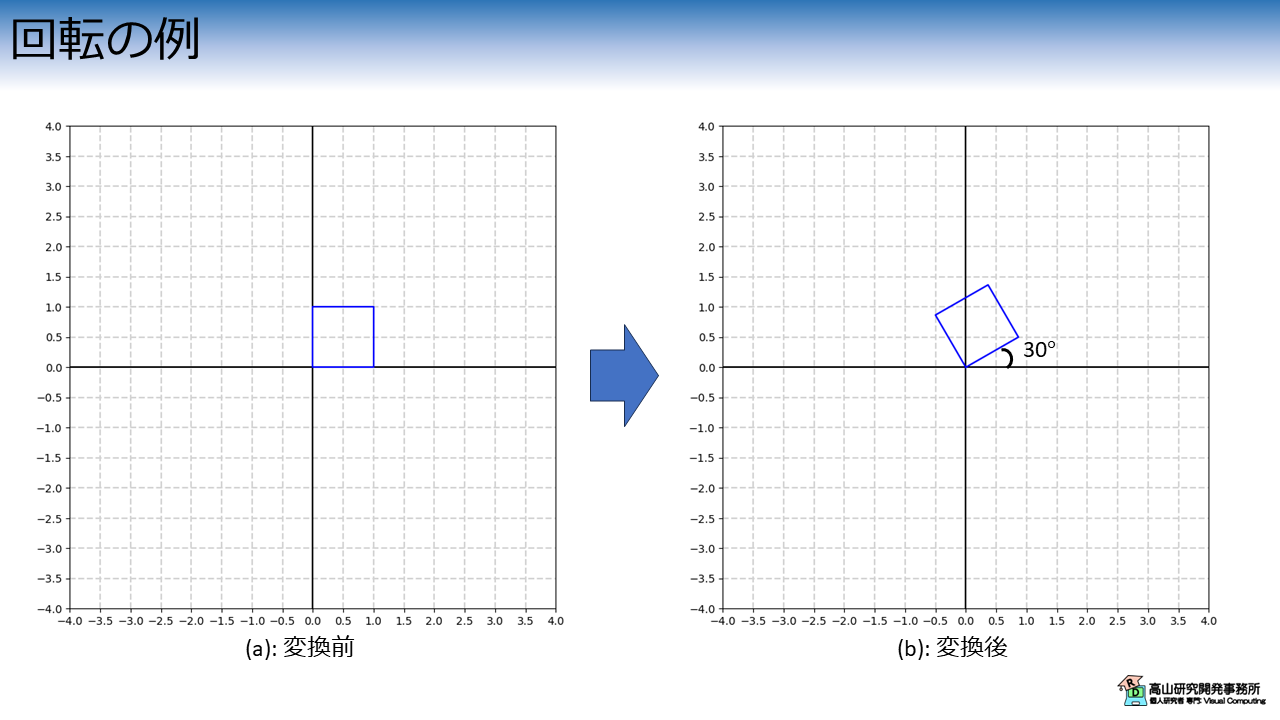
図5は反時計周りに$\theta = 30^{\circ}$回転するアフィン変換を適用した例です．
変換式は次の式で表されます．

$$ \begin{equation} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} \cos (30^{\circ}) & -\sin (30^{\circ}) & 0 \\ \sin (30^{\circ}) & \cos (30^{\circ}) & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{equation} $$

単純な四角形に対して回転を適用した例を示しています．画像直前の文章で処理内容を説明しています． — 回転の例

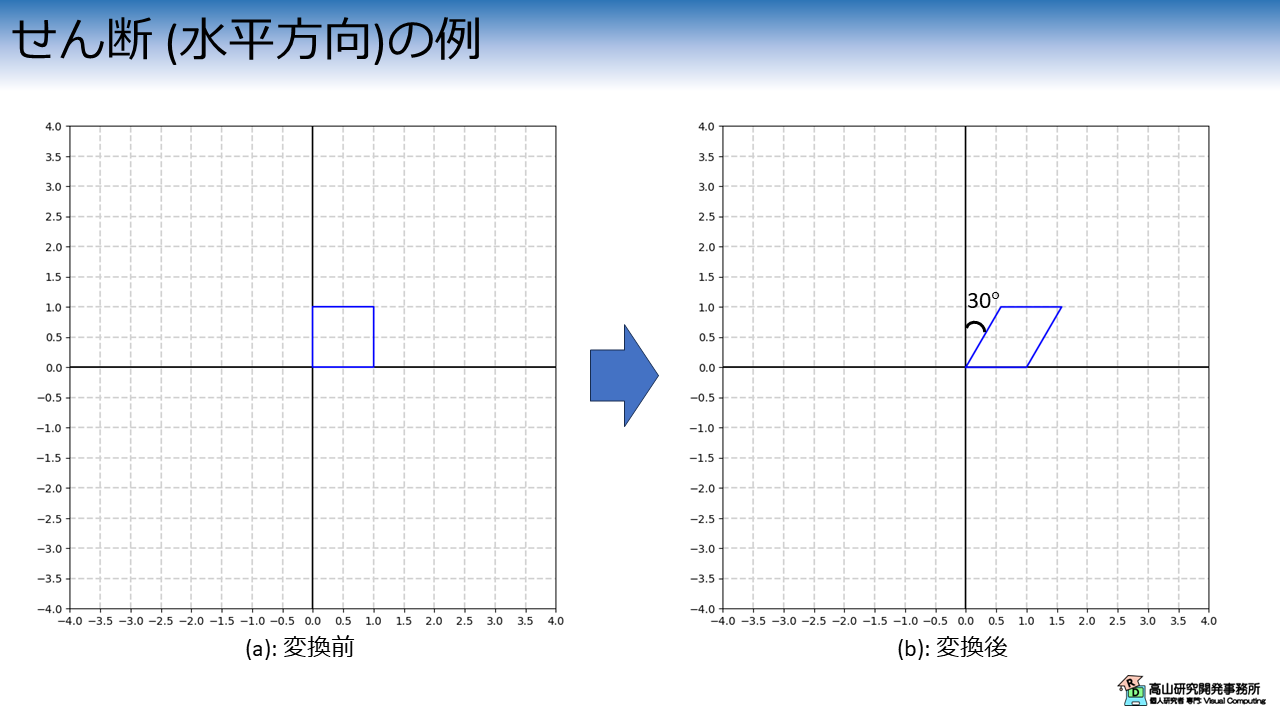
せん断 (水平方向)

せん断については，水平方向の変換と鉛直方向の変換に分けてお見せした方が分かりやすいと思うので，まずは水平方向のせん断から紹介します．
$y$軸から水平方向に$\theta$だけずらすアフィン変換は次の式で表されます．

$$ \begin{equation} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & \tan (\theta) & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{equation} $$

図6は$y$軸から水平方向に$30^{\circ}$だけずらすアフィン変換を適用した例です．
変換式は次の式で表されます．

$$ \begin{equation} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & \tan (30^{\circ}) & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{equation} $$

単純な四角形に対して水平方向のせん断を適用した例を示しています．画像直前の文章で処理内容を説明しています． — せん断 (水平方向) の例

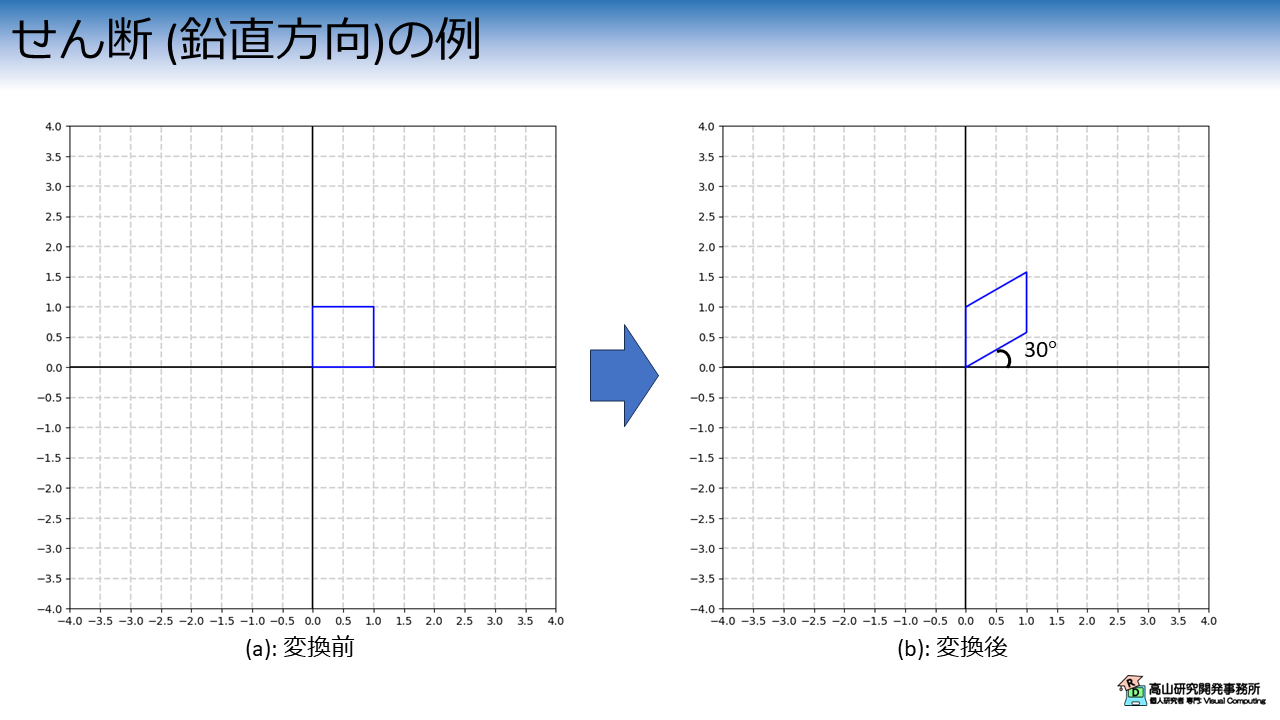
せん断 (鉛直方向)

次に，鉛直方向のせん断を紹介します．
$x$軸から鉛直方向に$\theta$だけずらすアフィン変換は次の式で表されます．

$$ \begin{equation} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ \tan (\theta) & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{equation} $$

図7は$x$軸から鉛直方向に$30^{\circ}$だけずらすアフィン変換を適用した例です．
変換式は次の式で表されます．

$$ \begin{equation} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ \tan (30^{\circ}) & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{equation} $$

単純な四角形に対して鉛直方向のせん断を適用した例を示しています．画像直前の文章で処理内容を説明しています． — せん断 (鉛直方向) の例

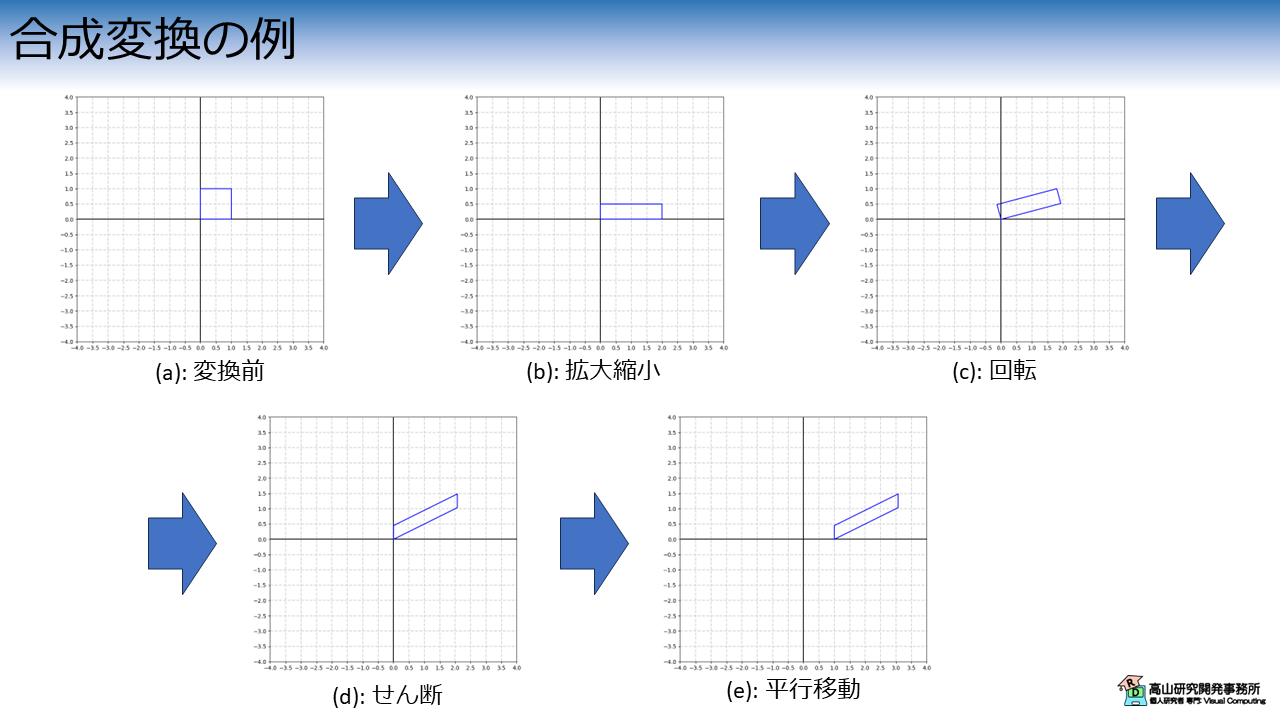
合成変換

冒頭で述べたとおり，アフィン変換は複数の変換を組み合わせる (合成変換と言います) ことで複雑な変換を行うことができます．
図8は拡大縮小 $\rightarrow$ 回転 $\rightarrow$ せん断 $\rightarrow$ 平行移動の順で変換を適用した例を示しています．
この変換は次の式に示すような合成変換になります．

$$ \begin{eqnarray} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} & = & \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & \tan (\theta_s) & 0 \\ \tan (\theta_s) & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \cos (\theta_r) & -\sin (\theta_r) & 0 \\ \sin (\theta_r) & \cos (\theta_r) & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \nonumber \\ & = & \boldsymbol{A'} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{eqnarray} $$

$(x\ y\ 1)^{\mathbb{T}}$に適用される順に，右から変換行列が並んでいる点に注意してください．
変換行列の順番を入れ替えた場合は，異なる変換結果が得られます．

単純な四角形に対して合成変換を適用した例を示しています．画像直前の文章で処理内容を説明しています． — 合成変換の例

対象物の中心を変換軸とする変換

図5に示した回転の例が分かりやすいと思いますが，線型変換は原点を軸として作用します．
一方実用上では，図2に示した追跡点への適用例のように対象物の特定の点を軸として変換を行う場合が多いです．

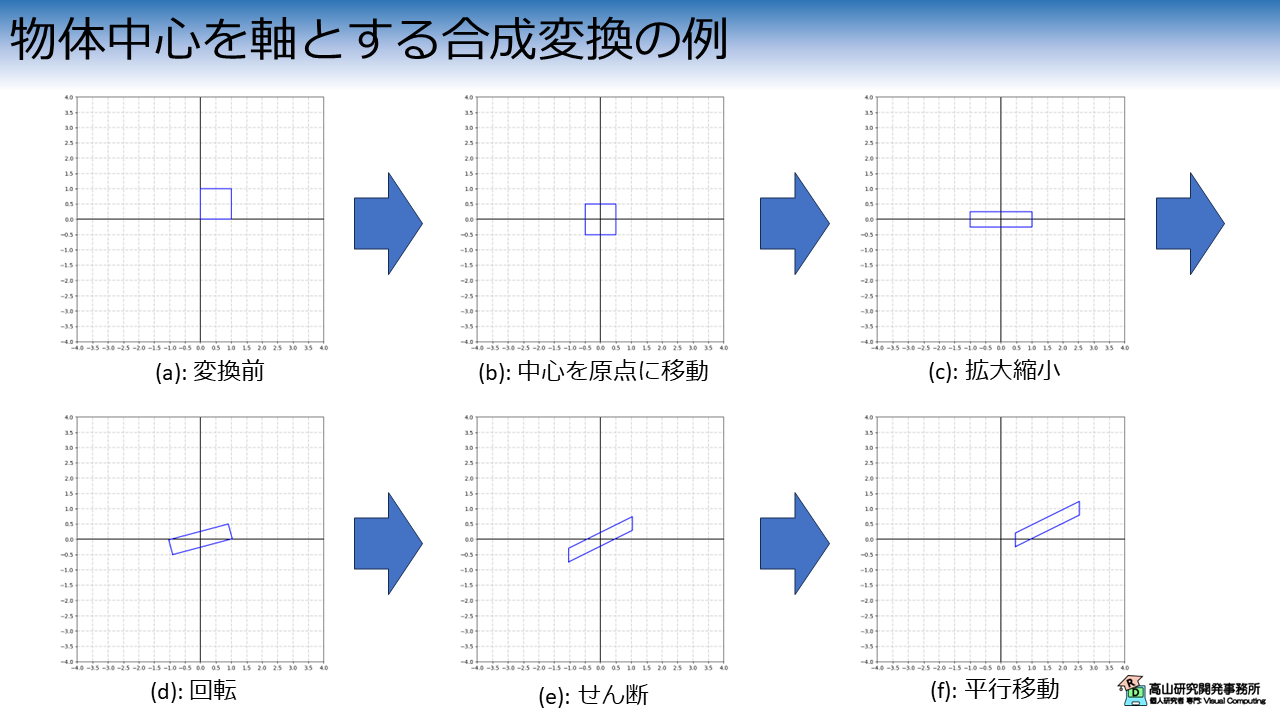
このような処理を行うには，図9に示すように線型変換の前に変換の軸となる点を原点に移動させ，その後に線型変換を行います．
平行移動を行う場合は，最初に行った原点への移動を考慮して移動量を調整することで所望の位置へ移動させることができます．

単純な四角形に対して，物体中心を変換軸として合成変換を適用した例を示しています．画像直前の文章で処理内容を説明しています． — 物体中心を基点とする合成変換の例

3. 追跡点配列への適用例

最後に，動画から抽出した追跡点配列全体に対してアフィン変換を施した例を図10に示します．
特殊ケースを除いて (カメラが動く場面のシミュレートなど)，データ拡張を目的として追跡点配列にアフィン変換を適用する場合は全フレームに対して同じ変換を行います．
対象が動画になることで実装上難しくなる点は特にありませんが，どの程度の変換を行うかは認識性能に影響します．
変換後の追跡点がどのような状態になっているかは確認しておくことが重要です．

(a): 変換前

(b): 変換後

追跡点動画のアフィン変換例

今回はアフィン変換を用いて追跡点の変形を行う方法を紹介しましたが，如何でしたでしょうか?
アフィン変換は単純な処理ですが，変換の組み合わせとパラメータ次第で様々な変形が行なえます．

今回は2次元平面上のアフィン変換を紹介させていただきましたが，3次元空間上の変換も同じような処理で行えます．
手話認識の場面では現状あまり使われていませんが (奥行方向の精度が良くないのと，カメラ位置が正面で固定の場合が多いので)，3次元空間上のアフィン変換もいずれ試してみたいと思います．

なお，アフィン変換は使う分には簡単ですが，数学的な話を理解しようとすると幾何学に真面目に取り組む必要があります．
今回の記事を執筆するにあたってサクッと調べ直そうと思ったのですが，かなり苦戦しました．
(そして，その苦労はあまり記事に反映されていません(^^;))
ご興味のある方は英語のWikipediaや射影幾何学についての解説をしているサイトなど [Wiki'24, Birchfield'98, 出口'90, 小室'18] を見てみると面白いかもしれません．

今回紹介した話が，動作追跡向けの前処理などについて悩んでいる方に何か参考になれば幸いです．

[Wiki'24]: "Affine transformation", available here, 2024.
[Birchfield'98]: S. Birchfield, "An Introduction to Projective Geometry (for computer vision)," available here, 1998.
[出口'90]: 出口光一郎，"コンピュータビジョン，グラフィックスのための射影幾何学[1]，" 計測と制御，Vol.29, No.11, here, 1990.
[小室'18]: 小室久二郎，"初等数学入門 - 射影幾何学，" available here, 2018.

アフィン変換による骨格追跡点の変形方法

This image is generated with ChatGPT-4, and edited by the author.

作成日:2023年10月13日(金) 00:00

最終更新日:2024年10月07日(月) 11:28

カテゴリ:コンピュータビジョン