アフィン変換による骨格追跡点の変形方法・JAX編

This image is generated with ChatGPT-4, and edited by the author.
作成日:2023年11月13日(月) 00:00
最終更新日:2024年10月07日(月) 11:54
カテゴリ:コンピュータビジョン
タグ:  アフィン変換 JAX MediaPipe 動作解析 手話認識 骨格追跡 Python

アフィン変換による骨格追跡点変形処理を，JAXで実装する方法を紹介します．

目次

こんにちは．高山です．
以前の記事で，Numpyを用いてアフィン変換を骨格追跡点に適用して変形する方法を紹介しました．
今回は，同様の処理をJAXを用いて実装してみたいと思います．
今回解説するスクリプトはGitHub上に公開しています．

なお，Tensorflowの記事で，計算グラフの再トレーシングという問題について紹介しました．
上記の問題はJAXにも存在しており，現在のところ上手い回避方法が実装できておりません(^^;)．
予めご了承ください (どなたか妙案をご存知の方がいれば教えていただきたいです(^^;))．

更新履歴 (大きな変更のみ記載しています)

  • 2024/09/17: タイトル，タグ，サマリを更新しました

1. モジュールのインストールとロード

まず最初に，下記のコードでモジュールをロードします．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
# Standard modules.
import gc
import sys
import time
from functools import partial

# CV/ML.
import numpy as np

import jax
import jax.numpy as jnp
from jax import jit

【コード解説】
- 標準モジュール
  - gc: ガベージコレクション用ライブラリ
    処理時間計測クラスの内部処理で用います．
  - sys: Pythonシステムを扱うライブラリ
    今回はバージョン情報を取得するために使用しています．
  - time: 時刻データを取り扱うためのライブラリ
    今回は処理時間を計測するために使用しています．
  - functools: 関数オブジェクトを操作するためのライブラリ
    処理時間計測クラスに渡す関数オブジェクト作成に使用しています．
- 計算処理用モジュール
  - numpy: 行列演算ライブラリ．今回はデータをロードするために使用します．
  - jax: JAXライブラリのルート
  - jax.numpy: JAXベースの行列演算モジュール．Numpyと同様の関数群を持ちます．
  - jax.jit: Just in Time コンパイル用のモジュール．
    実装した処理をコンパイルして Define-and-Run ベースで動かすために使用します．

記事執筆時点のPythonと主要モジュールのバージョンは下記のとおりです．

1
2
3
print(f"Python:{sys.version}")
print(f"Numpy:{np.__version__}")
print(f"JAX:{jax.__version__}")

Python:3.10.12 (main, Jun 11 2023, 05:26:28) [GCC 11.4.0]
Numpy:1.23.5
JAX:0.4.16

2. データのロードと確認

次に，下記の処理で変換前と変換後の追跡点データをダウンロードします．
変換後の追跡点データはNumpy編で紹介した処理で生成したデータです．
このデータは今回の処理で生成したデータとの比較に用います．

!wget https://github.com/takayama-rado/trado_samples/raw/main/test_data/finger_far0_non_static.npy
!wget https://github.com/takayama-rado/trado_samples/raw/main/test_data/finger_far0_non_static_affine.npy

ls コマンドでデータがダウンロードされているか確認します．

!ls
finger_far0_non_static_affine.npy  finger_far0_non_static.npy  sample_data

3. 実験用処理の実装

実験に先立って，処理時間計測用の関数と実験用定数を定義します．
次のコードは処理時間の値から，適切なSI接頭辞を設定し，文字列にして返します．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
def get_perf_str(val):
    token_si = ["", "m", "µ", "n", "p"]
    exp_si = [1, 1e3, 1e6, 1e9, 1e12]
    perf_str = f"{val:3g}s"
    si = ""
    sval = val
    for token, exp in zip(token_si, exp_si):
        if val * exp > 1.0:
            si = token
            sval = val * exp
            break
    perf_str = f"{sval:3g}{si}s"
    return perf_str

- 引数
  - val: 処理時間を示す値 (秒)
- 2-6行目: 変数の初期化
- 7-11行目: 接頭辞を選択して，表示値を調整
- 12行目: 表示文字列を作成

次のコードは，処理時間を格納した配列から統計量を求めて表示します．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
def print_perf_time(intervals, top_k=None):
    if top_k is not None:
        intervals = np.sort(intervals)[:top_k]
    min = intervals.min()
    max = intervals.max()
    mean = intervals.mean()
    std = intervals.std()

    smin = get_perf_str(min)
    smax = get_perf_str(max)
    mean = get_perf_str(mean)
    std = get_perf_str(std)
    if top_k:
        print(f"Top {top_k} summary: Max {smax}, Min {smin}, Mean +/- Std {mean} +/- {std}")
    else:
        print(f"Overall summary: Max {smax}, Min {smin}, Mean +/- Std {mean} +/- {std}")

- 引数:
  - intervals: 処理時間のNumpy配列
  - top_k: intervalsから，処理時間が短いサンプルをk個取り出して統計量を算出
- 2-3行目: Top K個のサンプル抽出
- 4-7行目: 統計量算出
- 9-16行目: 表示文字列を作成して表示

次のクラスは，入力した関数を複数回呼び出して，処理時間の統計量を表示します．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class PerfMeasure():
    def __init__(self,
                 trials=100,
                 top_k=10):
        self.trials = trials
        self.top_k = top_k

    def __call__(self, func):
        gc.collect()
        gc.disable()
        intervals = []
        for _ in range(self.trials):
            start = time.perf_counter()
            func()
            end = time.perf_counter()
            intervals.append(end - start)
        intervals = np.array(intervals)
        print_perf_time(intervals)
        if self.top_k:
            print_perf_time(intervals, self.top_k)
        gc.enable()
        gc.collect()

- 引数:
  - trials: 入力関数の実行回数
  - top_k: 値が定義されている場合，全体の処理時間配列から処理時間が短いサンプルをk個取り出して統計量を算出
- 9-10行目: 計測中はガベージコレクションをしないように設定
- 11-20行目: 処理時間計測処理
- 21-22行目: ガベージコレクションの設定を元に戻す

最後に，次のコードで実験用の定数を定義して処理時間計測クラスをインスタンス化しています．

1
2
3
TRIALS = 100
TOPK = 10
pmeasure = PerfMeasure(TRIALS, TOPK)

実際の所，Colabの様な複雑な処理環境で他のプロセスの影響を排除して純粋な処理時間を計測するのはかなり難しいです．
そこでここでは，処理の繰り返し数を \(100\) とし全体の統計量に加えて，処理時間の短い代表値 \(10\) 試行からも統計量を表示するようにしています．

4. アフィン変換の実装

ここから先は変換処理の実装・実行を行います．
TensorflowやPyTorchと同じく，JAXもプログラムの実行時に処理をコンパイル (計算グラフの作成) して実行します．
現在のJAXには，下記に示すとおり2種類の計算グラフ作成方法があります．

  • Define-by-Run: データを入力した際に処理のコンパイルと実行を同時に行う．
    Pythonの実行環境と親和性が高くインタラクティブな実行環境で利用しやすくなっています．
  • Define-and-Run (JITコンパイル): (C言語のように) 処理のコンパイルと実行が明確に別れて行われる．
    処理の最適化性能が高いため高速に動作します．

今回は，変換処理をそれぞれの計算グラフ作成方法で実行して処理時間を比較してみたいと思います．

4.1. Define-by-run に基づく実装

本項ではまず，Define-by-run を用いた場合の実装を紹介します．
以前の記事の後半で紹介した，対象物内の特定位置を変換軸とする変換を実装していきます．

変換行列の算出処理

次のコードは，入力パラメータに応じた変換行列を算出する関数を実装しています．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def get_affine_matrix_2d_jax(center,
                             trans,
                             scale,
                             rot,
                             skew,
                             dtype=jnp.float32):
    center_m = jnp.array([[1.0, 0.0, -center[0]],
                          [0.0, 1.0, -center[1]],
                          [0.0, 0.0, 1.0]])
    scale_m = jnp.array([[scale[0], 0.0, 0.0],
                         [0.0, scale[1], 0.0],
                         [0.0, 0.0, 1.0]])
    _cos = jnp.cos(rot)
    _sin = jnp.sin(rot)
    rot_m = jnp.array([[_cos, -_sin, 0.0],
                       [_sin, _cos, 0],
                       [0.0, 0.0, 1.0]])
    _tan = jnp.tan(skew)
    skew_m = jnp.array([[1.0, _tan[0], 0.0],
                        [_tan[1], 1.0, 0.0],
                        [0.0, 0.0, 1.0]])
    move = jnp.array(center) + jnp.array(trans)
    trans_m = jnp.array([[1.0, 0.0, move[0]],
                         [0.0, 1.0, move[1]],
                         [0.0, 0.0, 1.0]])
    # Make affine matrix.
    mat = jnp.identity(3, dtype=dtype)
    mat = jnp.matmul(center_m, mat)
    mat = jnp.matmul(scale_m, mat)
    mat = jnp.matmul(rot_m, mat)
    mat = jnp.matmul(skew_m, mat)
    mat = jnp.matmul(trans_m, mat)
    return mat.astype(dtype)

- 引数
  - center: 変換軸座標 `(center_x, center_y)`
    通常は物体中心位置や特定の追跡点位置を指定します．
  - trans: 平行移動量 `(trans_x, trans_y)`
  - scale: 拡大縮小量 `(scale_x, scale_y)`
  - rot: 回転量 (ラジアン)
    この値のみスカラーです．
  - skew: せん断量 (ラジアン) `(skew_x, skew_y)`
  - dtype: 出力データ型
- 7-26行目: 各変換行列を算出
  `center_m` の算出では，指定座標を原点に移動するためにマイナスをかけた値を移動量として設定しています．
  回転とせん断はラジアン値を入力として，それぞれ対応する三角関数を適用した値を設定しています．
  平行移動では，最初に行う指定座標の原点への移動をオフセットとして加えた値を移動量として設定しています．
- 28-32行目: 初めに`mat` を単位行列で初期化し，各変換行列を順次適用
- 33行目: `dtype` で指定した型に変換して値を返す

アフィン変換の適用処理

次のコードは，追跡点配列に変換行列を適用する関数を実装しています．

1
2
3
4
5
6
7
def apply_affine_jax(inputs, mat):
    # Apply transform.
    xy = inputs[:, :, :2]
    xy = jnp.concatenate([xy, jnp.ones([xy.shape[0], xy.shape[1], 1])], axis=-1)
    xy = jnp.einsum("...j,ij", xy, mat)
    inputs = inputs.at[:, :, :2].set(xy[:, :, :-1])
    return inputs

- 引数:
  - inputs: 追跡点配列 `[T, J, C]`
    - T: 動画フレームインデクス
    - J: 追跡点インデクス
    - C: 特徴量インデクス．今回は $(x, y, z, c)$ の4次元特徴量を用いています．
  - mat: アフィン変換行列 `[3, 3]`
- 2-4行目: 追跡点配列から $(x, y)$ 座標列を取り出して，特徴量次元の末尾に $1$ を加えて同次座標形式に変換
- 5行目: `xy` の特徴量次元に対してアフィン変換行列を適用
- 6-7行目: 変換後の$(x, y)$ 座標列を `inputs` に代入して返す

5行目の変換行列の適用では，Numpy版と同様にアインシュタインの縮約表記を用いた演算を行っています．
Einsum についてはこちらに簡単な解説記事を用意しています．
ご一読いただければうれしいです．

アフィン変換の実行

次のコードでは，追跡点を trackdata にロードして，関数の仕様に合わせて形状を変更しています．
今回用いるデータは [P, T, J, C] 形状 ( P は人物インデクス) の配列ですが，動画に映っている人物は1名だけですので P 軸は除去しています．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
# Load data.
trackfile = "./finger_far0_non_static.npy"
reffile = "./finger_far0_non_static_affine.npy"
trackdata = np.load(trackfile).astype(np.float32)
refdata = np.load(reffile).astype(np.float32)
print(trackdata.shape)

# Remove person axis.
trackdata = trackdata[0]
refdata = refdata[0]

# Convert to jnp.array
trackdata = jnp.array(trackdata)
refdata = jnp.array(refdata)

次のコードでは，アフィン変換行列の設定パラメータを次のように指定しています．

  • 変換軸座標: \((C_x, C_y) = (638.0, 389.0)\)，おおよそ両肩の中心になる座標を指定しています．
  • 平行移動量: \((T_x, T_y) = (100.0, 0.0)\)
  • 拡大縮小量: \((S_x, S_y) = (2.0, 0.5)\)
  • 回転量: \(R = \pi * 15.0 / 180.0\)
  • せん断量: \((K_x, K_y) = \pi * (15.0, 15.0) / 180.0\)

回転量とせん断量はラジアンになってます．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
 # Get affine matrix.
center = jnp.array([638.0, 389.0])
trans = jnp.array([100.0, 0.0])
scale = jnp.array([2.0, 0.5])
rot = float(jnp.radians(15.0))
skew = jnp.radians(jnp.array([15.0, 15.0]))
dtype = jnp.float32
print("Parameters")
print("Center:", center)
print("Trans:", trans)
print("Scale:", scale)
print("Rot:", rot)
print("Skew:", skew)

print処理の結果を示します．

Parameters
Center: [638. 389.]
Trans: [100.   0.]
Scale: [2.  0.5]
Rot: 0.2617993950843811
Skew: [0.2617994 0.2617994]

では，アフィン変換処理を実行していきます．
まず次のコードで処理時間計測クラスに入力するためのラッパー関数を定義します．

1
2
3
def perf_wrap_func(trackdata, center, trans, scale, rot, skew, dtype):
    mat = get_affine_matrix_2d_jax(center, trans, scale, rot, skew, dtype=dtype)
    newtrack = apply_affine_jax(trackdata, mat)

次のコードは先程実装した変換処理にtrackdataを入力して，変換後の追跡点newtrackを得ています．
1回目の処理呼び出しでは，処理のコンパイルが行われるため個別に時間を計測し，参照用の変換後追跡点との誤差を計測しています．
その後，処理時間計測クラスを用いて平均処理時間を表示しています．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
testtrack = trackdata.copy()

# The 1st call may be slow because of the computation graph construction.
print(f"Time of first call.")
start = time.perf_counter()
mat = get_affine_matrix_2d_jax(center, trans, scale, rot, skew, dtype=dtype)
newtrack = apply_affine_jax(testtrack, mat)
interval = time.perf_counter() - start
print_perf_time(np.array([interval]))

# Evaluate difference.
diff = (jnp.round(newtrack) - jnp.round(refdata)).sum()
print(f"Sum of error:{diff}")

testtrack = trackdata.copy()

print("Time after second call.")
target_fn = partial(perf_wrap_func,
                    trackdata=testtrack,
                    center=center, trans=trans, scale=scale, rot=rot, skew=skew,
                    dtype=dtype)
pmeasure(target_fn)

print 処理の結果を示します．
1回目の処理時間は662.2ミリ秒程度で，誤差はありませんでした．
2回目以降の処理では，(他のプロセスの影響が少ない場合は) 17.5ミリ秒程度で処理が完了しています．

Time of first call.
Overall summary: Max 662.249ms, Min 662.249ms, Mean +/- Std 662.249ms +/-   0s
Sum of error:0.0
Time after second call.
Overall summary: Max 115.266ms, Min 17.1939ms, Mean +/- Std 36.2639ms +/- 16.9179ms
Top 10 summary: Max 17.8094ms, Min 17.1939ms, Mean +/- Std 17.4581ms +/- 166.24µs

入力データ形状が変わった場合の挙動

Tensorflowの記事と同じく，今回も入力データの形状が変わった場合の挙動を調査してみたいと思います．
次のコードは先程のアフィン変換の実行処理とほぼ同じですが，入力データの時間長が1フレーム分短くなっています．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
testtrack = trackdata.copy()

# The 1st call may be slow because of the computation graph construction.
print(f"Time of first call.")
start = time.perf_counter()
mat = get_affine_matrix_2d_jax(center, trans, scale, rot, skew, dtype=dtype)
newtrack = apply_affine_jax(testtrack[:-1], mat)
interval = time.perf_counter() - start
print_perf_time(np.array([interval]))

testtrack = trackdata.copy()

print("Time after second call.")
target_fn = partial(perf_wrap_func,
                    trackdata=testtrack[:-1],
                    center=center, trans=trans, scale=scale, rot=rot, skew=skew,
                    dtype=dtype)
pmeasure(target_fn)

print 処理の結果を示します．
1回目の処理では324.2ミリ秒程度，2回目以降の処理では29.4ミリ秒程度となり，JAXでは処理の再トレーシングが起きているようです．

output
Time of first call.
Overall summary: Max 324.22ms, Min 324.22ms, Mean +/- Std 324.22ms +/-   0s
Time after second call.
Overall summary: Max 142.864ms, Min 27.1088ms, Mean +/- Std 65.1514ms +/- 26.8165ms
Top 10 summary: Max 30.4011ms, Min 27.1088ms, Mean +/- Std 29.4172ms +/- 961.927µs

4.2. Define-and-run に基づく実装

ここから先は，Define-and-run を用いた場合の挙動について見ていきます．

JAXでは，関数を @jax.jit デコレータで修飾することで Define-and-Run に基づいて計算グラフを作成することができます．
今回は Define-and-Run で動作するように変換処理を実装しているので，コードの変更はほとんどありません．

変換行列の算出処理

次のコードでは，先程紹介した変換行列処理関数を Define-and-run で動作するようにしています．
中身のコードは完全に同じなのでここでは説明を省かさせていただきます．

1
2
3
4
5
6
7
@jit
def get_affine_matrix_2d_jax_jit(center,
                                 trans,
                                 scale,
                                 rot,
                                 skew):
    ...

アフィン変換の適用処理

次のコードは，追跡点配列に変換行列を適用する関数を実装しています．
中身のコードは完全に同じなのでここでは説明を省かさせていただきます．

1
2
3
@jit
def apply_affine_jax_jit(inputs, mat):
    ...

アフィン変換の実行

アフィン変換を実行します．
まず次のコードで処理時間計測クラスに入力するためのラッパー関数を定義します．

1
2
3
def perf_wrap_func(trackdata, center, trans, scale, rot, skew):
    mat = get_affine_matrix_2d_jax_jit(center, trans, scale, rot, skew)
    newtrack = apply_affine_jax_jit(trackdata, mat)

次のコードで変換処理を実行しています．
先程と同じく，1回目の処理呼び出しでは，処理のコンパイルが行われるため個別に時間を計測し，2回目以降に処理時間計測クラスを用いて平均時間を表示しています．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
testtrack = trackdata.copy()

# The 1st call may be slow because of the computation graph construction.
print(f"Time of first call.")
start = time.perf_counter()
mat = get_affine_matrix_2d_jax_jit(center, trans, scale, rot, skew)
newtrack = apply_affine_jax_jit(testtrack, mat)
interval = time.perf_counter() - start
print_perf_time(np.array([interval]))

# Evaluate difference.
diff = (jnp.round(newtrack) - jnp.round(refdata)).sum()
print(f"Sum of error:{diff}")

testtrack = trackdata.copy()

print("Time after second call.")
target_fn = partial(perf_wrap_func,
                    trackdata=testtrack,
                    center=center, trans=trans, scale=scale, rot=rot, skew=skew)
pmeasure(target_fn)

print 処理の結果を示します．
1回目の処理では445.7ミリ秒程度かかっていますが，2回目以降の処理では1.3ミリ秒程度で処理が完了していることが分かります．

Time of first call.
Overall summary: Max 445.719ms, Min 445.719ms, Mean +/- Std 445.719ms +/-   0s
Sum of error:0.0
Time after second call.
Overall summary: Max 14.5279ms, Min 1.23261ms, Mean +/- Std 2.41537ms +/- 2.43119ms
Top 10 summary: Max 1.36594ms, Min 1.23261ms, Mean +/- Std 1.2714ms +/- 43.6211µs

入力データ形状が変わった場合の挙動

次に，先程と同じく入力データの形状が変わった場合の挙動を示します．
次のコードは先程の変換実行処理とほぼ同じですが，入力データの時間長が1フレーム分短くなっています．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
testtrack = trackdata.copy()

# The 1st call may be slow because of the computation graph construction.
print(f"Time of first call.")
start = time.perf_counter()
mat = get_affine_matrix_2d_jax_jit(center, trans, scale, rot, skew)
newtrack = apply_affine_jax_jit(testtrack[:-1], mat)
interval = time.perf_counter() - start
print_perf_time(np.array([interval]))

# Evaluate difference.
diff = (jnp.round(newtrack) - jnp.round(refdata[:-1])).sum()
print(f"Sum of error:{diff}")

testtrack = trackdata.copy()

print("Time after second call.")
target_fn = partial(perf_wrap_func,
                    trackdata=testtrack[:-1],
                    center=center, trans=trans, scale=scale, rot=rot, skew=skew)
pmeasure(target_fn)

print 処理の結果を示します．
1回目の処理では165.0ミリ秒程度，2回目以降の処理では1.3ミリ秒程度となり，JAXでは入力長が変化することで再トレーシングが起きることが分かります．

Time of first call.
Overall summary: Max 164.981ms, Min 164.981ms, Mean +/- Std 164.981ms +/-   0s
Sum of error:0.0
Time after second call.
Overall summary: Max 8.83706ms, Min 1.21181ms, Mean +/- Std 2.05039ms +/- 1.7484ms
Top 10 summary: Max 1.34863ms, Min 1.21181ms, Mean +/- Std 1.26267ms +/- 44.5478µs

5. データ拡張用途として，ランダムな変換を行う方法

第5節では，アフィン変換をデータ拡張に応用する方法を紹介します．
処理の流れを図1に示します．

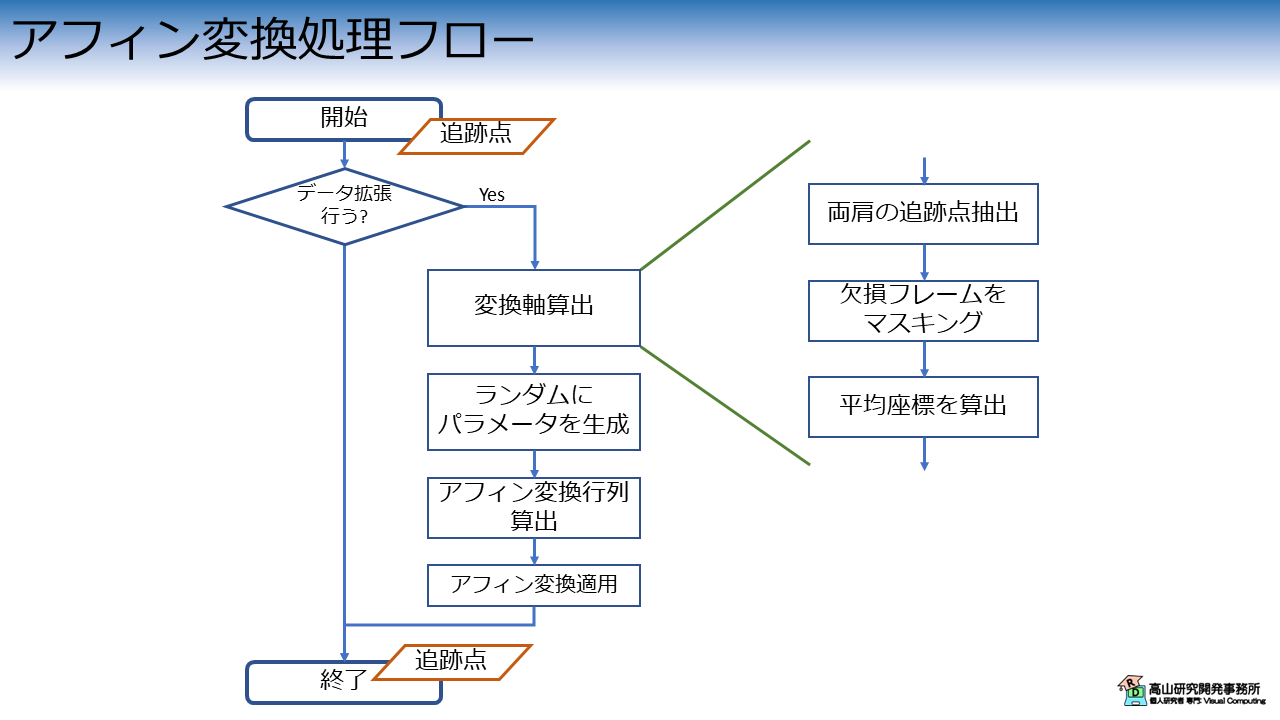
追跡データに対して，ランダムなパラメータでアフィン変換を適用する処理のフローチャートです．画像に続いて説明があります．
アフィン変換処理フロー

変換処理自体は，次の3個の処理から構成されます．

  1. 変換軸算出と変換パラメータの生成
  2. 変換行列の算出
  3. アフィン変換の適用

また，データ拡張に応用する場合は，変換を適用するかどうかを確率的に決める処理が入る場合が多いです．

今回はJAXを用いているので，より高速な動作が期待できる Define-and-run を用いた実装形態を紹介したいと思います．
具体的には，次の図2に示す2種類の実装形態を紹介します．

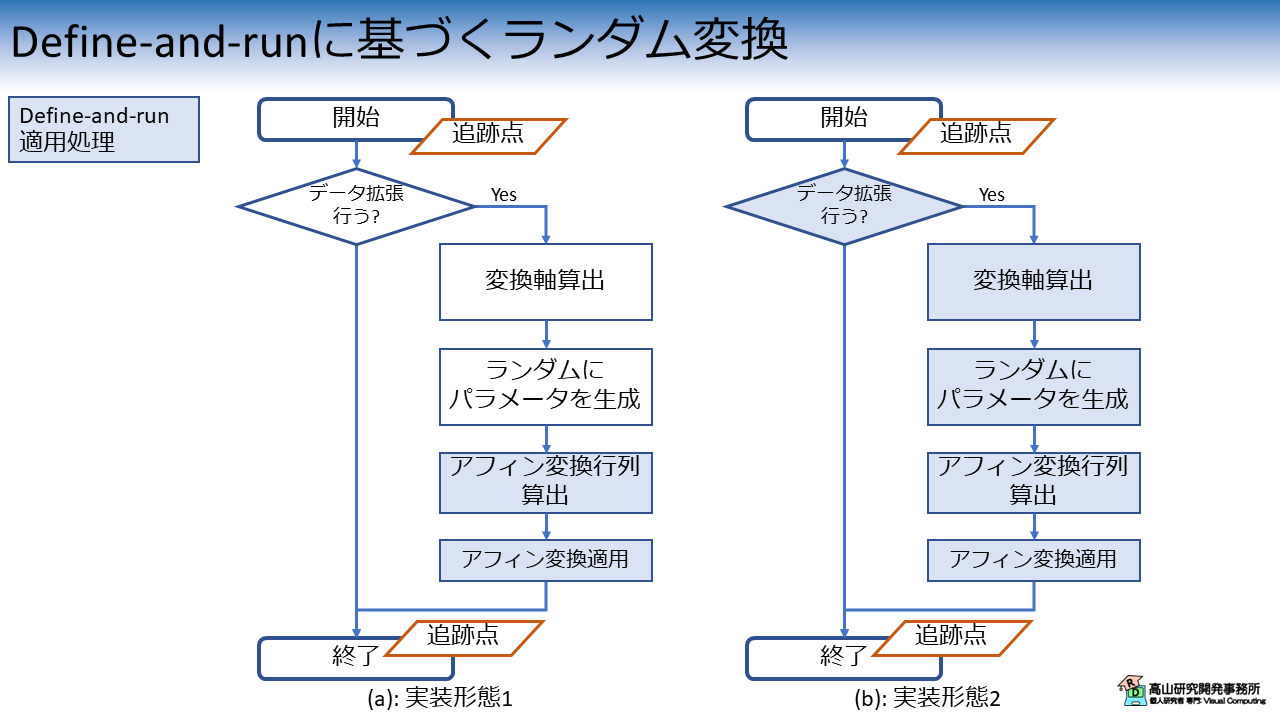
JAXを用いたアフィン変換の処理フローチャートです．左側にはNumpy版と同様の標準的な実装形態を示しています．右側にはDefine-and-runに基づく高速な実装形態を示しています．各実装形態の説明は次項以降の文章で行っています．
Define-and-runに基づくランダム変換

図2(a) に示す一つ目の実装形態では，全体の処理は通常のPythonプロセスを用いて組み，PythonプロセスからJITコンパイルをした関数を読み出します．
こちらの実装は比較的単純で，Numpy版の実装と同様の処理構成が維持できます．

図2(b) に示す２つ目の実装形態では，分岐やランダムパラメータの生成を含んだ処理全体をJITコンパイルします．
こちらの実装では，コンパイル可能な形に処理構成を変更する必要があります．

では，次項から具体的な処理を説明していきます．

5.1 実装形態1: PythonプロセスからJITコンパイルをした関数を呼び出す

データ拡張クラス

図2(a) に示した処理を実装したクラスが次のコードになります．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class RandomAffineTransform2D_JAX():
    def __init__(self,
                 center_joints,
                 apply_ratio,
                 trans_range,
                 scale_range,
                 rot_range,
                 skew_range,
                 random_seed=None):
        self.center_joints = center_joints
        self.apply_ratio = apply_ratio
        self.trans_range = trans_range
        self.scale_range = scale_range
        self.rot_range = jnp.radians(jnp.array(rot_range))
        self.skew_range = jnp.radians(jnp.array(skew_range))
        if random_seed is not None:
            self.rng = jax.random.PRNGKey(random_seed)
        else:
            self.rng = jax.random.PRNGKey(0)

    def gen_uniform_and_update_key(self, low=0.0, high=1.0, shape=(1,)):
        # Generate random value.
        val = jax.random.uniform(self.rng, shape)
        # Scale to target range.
        val = (high - low) * val + low
        # Update key.
        self.rng = jax.random.split(self.rng, num=1)[0]
        return val

    def __call__(self, inputs):
        if self.gen_uniform_and_update_key() >= self.apply_ratio:
            return inputs

        # Calculate center position.
        temp = inputs[:, self.center_joints, :]
        temp = temp.reshape([inputs.shape[0], -1, inputs.shape[-1]])
        mask = jnp.sum(temp, axis=(1, 2)) != 0
        # Use x and y only.
        center = temp[mask].mean(axis=0).mean(axis=0)[:2]

        trans = self.gen_uniform_and_update_key(
            self.trans_range[0], self.trans_range[1], (2,))
        scale = self.gen_uniform_and_update_key(
            self.scale_range[0], self.scale_range[1], (2,))
        rot = self.gen_uniform_and_update_key(
            self.rot_range[0], self.rot_range[1], (1,))[0]
        skew = self.gen_uniform_and_update_key(
            self.skew_range[0], self.skew_range[1], (2,))

        # Calculate matrix.
        mat = get_affine_matrix_2d_jax_jit(center, trans, scale, rot, skew)

        # Apply transform.
        inputs = apply_affine_jax_jit(inputs, mat)
        return inputs

- 引数
  - center_joints: 変換軸座標算出に使用する追跡点インデクス．
    ここで指定した追跡点の重心 (の全フレーム平均) が変換軸になります．
  - apply_ratio: 変換を適用する確率，[0.0, 1.0]で指定
  - trans_range: 平行移動量の範囲 `(minimum, maximum)`
  - scale_range: 拡大縮小量の範囲 `(minimum, maximum)`
  - rot_range: 回転量の範囲，度数で指定 `(minimum, maximum)`
  - skew_range: せん断量の範囲，度数で指定 `(minimum, maximum)`
  - random_seed: 疑似乱数生成器のシード，`None`の場合は`0`とする
- 10-19行目: クラスのインスタンス化処理
  16-19行目では疑似乱数生成器を生成しています．`random_seed` が指定されている場合は
  その値を用いて生成し，`None` の場合は`0`固定値を用います．
- 21-28行目: ランダム変数を生成し，次の生成時に異なる値を返すように生成器の鍵値を更新
- 30-55行目: ランダム変換処理
  - 31-32行目: 乱数を生成し，`apply_ratio` 以上だった場合は何もせずに値を返す
  - 35-39行目: 変換軸を算出
    まず初めに，`center_joints` で指定した追跡点配列を抽出します．
    次に，欠損フレームを除去するための `mask` を生成します．
    最後に，`mask` を適用した上で平均座標 (x, y) を算出し `center` としています．
  - 41-48行目: 指定した範囲で各変換パラメータをランダムに生成
  - 51行目: アフィン変換行列を算出
    ここでは先程実装した `get_affine_matrix_2d_jax_jit()` をクラスから呼び出すようにしています．
  - 54行目: アフィン変換適用
    ここでは先程実装した `apply_affine_jax_jit` をクラスから呼び出すようにしています．

データ拡張処理の実行

必要な処理が実装できましたので，処理を適用してみます．
まず，次のコードで変換クラスをインスタンス化します．

1
2
3
4
5
6
7
aug_fn = RandomAffineTransform2D_JAX(
    center_joints=[11, 12],
    apply_ratio=1.0,
    trans_range=[-100.0, 100.0],
    scale_range=[0.5, 2.0],
    rot_range=[-30.0, 30.0],
    skew_range=[-30.0, 30.0])

ここでは，center_joints に両肩の追跡点を指定しています．
この場合，変換軸は両肩の中央，つまり首元の座標になります．

次のコードでは，trackdata (のコピー) に対してランダムなパラメータで変換を施しています．
先程と同じく，1回目の処理呼び出しでは処理のコンパイルが行われるため個別に時間を計測し，2回目以降に処理時間計測クラスを用いて平均時間を表示しています．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
testtrack = trackdata.copy()

# The 1st call may be slow because of the computation graph construction.
print(f"Time of first call.")
start = time.perf_counter()
temp = aug_fn(testtrack)
interval = time.perf_counter() - start
print_perf_time(np.array([interval]))

testtrack = trackdata.copy()
print("Time after second call.")
target_fn = partial(aug_fn, inputs=testtrack)
pmeasure(target_fn)

print 処理の結果を示します．
1回目の処理では1.4秒程度かかっていますが，2回目以降の処理では6.9ミリ秒程度で処理が完了していることが分かります．

Time of first call.
Overall summary: Max 1.44494s, Min 1.44494s, Mean +/- Std 1.44494s +/-   0s
Time after second call.
Overall summary: Max 12.2906ms, Min 6.80869ms, Mean +/- Std 7.3811ms +/- 859.549µs
Top 10 summary: Max 6.9176ms, Min 6.80869ms, Mean +/- Std 6.86691ms +/- 41.6897µs

入力データ形状が変わった場合の挙動

第4節と同じく入力データの形状が変わった場合の挙動を示します．
次のコードは上の変換実行処理とほぼ同じですが，入力データの時間長が1フレーム分短くなっています．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
testtrack = trackdata.copy()

# The 1st call may be slow because of the computation graph construction.
print(f"Time of first call.")
start = time.perf_counter()
temp = aug_fn(testtrack[:-1])
interval = time.perf_counter() - start
print_perf_time(np.array([interval]))

testtrack = trackdata.copy()
print("Time after second call.")
target_fn = partial(aug_fn, inputs=testtrack[:-1])
pmeasure(target_fn)

print 処理の結果を示します．
1回目の処理は262.2ミリ秒程度で，2回目以降の処理では6.8ミリ秒程度でした．

Time of first call.
Overall summary: Max 262.183ms, Min 262.183ms, Mean +/- Std 262.183ms +/-   0s
Time after second call.
Overall summary: Max 12.4024ms, Min 6.62738ms, Mean +/- Std 7.4838ms +/- 1.09016ms
Top 10 summary: Max 6.83709ms, Min 6.62738ms, Mean +/- Std 6.77123ms +/- 66.6792µs

5.2 実装形態2: JITコンパイルを変換プロセス全体に適用

データ拡張クラス

次に，図2(b) に示した処理を実装したクラスを示します．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
class RandomAffineTransform2D_JAX_JIT():
    def __init__(self,
                 center_joints,
                 apply_ratio,
                 trans_range,
                 scale_range,
                 rot_range,
                 skew_range,
                 random_seed=None,
                 dtype=np.float32):
        self.center_joints = center_joints
        self.apply_ratio = apply_ratio
        self.trans_range = trans_range
        self.scale_range = scale_range
        self.rot_range = jnp.radians(jnp.array(rot_range))
        self.skew_range = jnp.radians(jnp.array(skew_range))
        self.dtype = dtype
        if random_seed is not None:
            self.rng = jax.random.PRNGKey(random_seed)
        else:
            self.rng = jax.random.PRNGKey(0)

    def gen_uniform_and_update_key(self, rng, low=0.0, high=1.0, shape=(2,)):
        # Generate random value.
        val = jax.random.uniform(rng, shape)
        # Scale to target range.
        val = (high - low) * val + low
        # Update key.
        rng = jax.random.split(rng, num=1)[0]
        return val, rng

    def apply(self, inputs, rng):
        # Calculate center position.
        temp = inputs[:, self.center_joints, :]
        temp = temp.reshape([inputs.shape[0], -1, inputs.shape[-1]])
        mask = jnp.sum(temp, axis=(1, 2)) != 0
        mask = mask.astype(self.dtype)

        temp = temp * mask[:, None, None]
        mask_sum = jnp.sum(mask)
        # `[T, J, C] -> [J, C] -> [C]`
        center = temp.sum(axis=0) / mask_sum
        center = center.mean(axis=0)
        # Use x and y only.
        center = center[:2]

        trans, rng = self.gen_uniform_and_update_key(rng,
            self.trans_range[0], self.trans_range[1], (2,))
        scale, rng = self.gen_uniform_and_update_key(rng,
            self.scale_range[0], self.scale_range[1], (2,))
        rot, rng = self.gen_uniform_and_update_key(rng,
            self.rot_range[0], self.rot_range[1], (2,))
        rot = rot[0]
        skew, rng = self.gen_uniform_and_update_key(rng,
            self.skew_range[0], self.skew_range[1], (2,))

        # Calculate matrix.
        mat = get_affine_matrix_2d_jax_jit(center, trans, scale, rot, skew)

        # Apply transform.
        inputs = apply_affine_jax_jit(inputs, mat)
        return inputs, rng

    @partial(jit, static_argnums=(0,))
    def affine_proc(self, inputs, rng):
        val, rng = self.gen_uniform_and_update_key(rng)
        retval, rng = jax.lax.cond(
            (val >= self.apply_ratio).astype(jnp.int32)[0],
            lambda: (inputs, rng),
            lambda: self.apply(inputs, rng))
        return retval, rng

    def __call__(self, inputs):
        rng = self.rng
        retval, rng = self.affine_proc(inputs, rng)
        self.rng = rng
        return retval

- 引数
  - center_joints: 変換軸座標算出に使用する追跡点インデクス．
    ここで指定した追跡点の重心 (の全フレーム平均) が変換軸になります．
  - apply_ratio: 変換を適用する確率，[0.0, 1.0]で指定
  - trans_range: 平行移動量の範囲 `(minimum, maximum)`
  - scale_range: 拡大縮小量の範囲 `(minimum, maximum)`
  - rot_range: 回転量の範囲，度数で指定 `(minimum, maximum)`
  - skew_range: せん断量の範囲，度数で指定 `(minimum, maximum)`
  - random_seed: 疑似乱数生成器のシード，`None`の場合は`0`とする
  - dtype: 出力データ型
- 11-21行目: クラスのインスタンス化処理
  18-21行目では疑似乱数生成器を生成しています．`random_seed` が指定されている場合は
  その値を用いて生成し，`None` の場合は`0`固定値を用います．
- 23-30行目: ランダム変数を生成し，次の生成時に異なる値を返すように生成器の鍵値を更新
- 32-62行目: ランダム変換処理
  - 34-45行目: 変換軸を算出
    まず初めに，`center_joints` で指定した追跡点配列を抽出します．
    次に，欠損フレームを除去するための `mask` を生成します．
    最後に，`mask` を適用した上で平均座標 (x, y) を算出し `center` としています．
    JAXのJIT関数内では，NumpyのようにBoolean配列を入力として部分配列を抽出することはできません．
    そこで，39-45行目に示す処理で平均座標を算出しています．
  - 47-55行目: 指定した範囲で各変換パラメータをランダムに生成
  - 58行目: アフィン変換行列を算出
    ここでは先程実装した `get_affine_matrix_2d_jax_jit()` をクラスから呼び出すようにしています．
  - 61行目: アフィン変換適用
    ここでは先程実装した `apply_affine_jax_jit` をクラスから呼び出すようにしています．
  - 62行目: 変換後の追跡点配列 `inputs` と更新後のランダム生成器の鍵値 `rng` を返す
- 64-71行目: JIT関数のエントリポイント
  まず初めに乱数 `rng` を生成します．
  次に，`jax.lax.cond()` を用いて次のように分岐処理を行います．
  - `rng` >= `apply_ratio`: 何もせずに `(inputs, rng)` を返します
  - `rng` < `apply_ratio`: `self.apply()` を呼び出し結果を返します
  どちらのケースでも結果は `retval` と `rng` に格納され，それらが戻り値になる点に注意してください．
  (このような実装がJITによって要求されます)
- 73-77行目: 変換処理のエントリポイント
  JIT関数はステートレスである必要があるので，JIT関数内部でランダム変数の格納はせず，ここで行っています．

Numpy版とは実装形態がかなり異なることが分かります．
これは主に，下記に示すJAXの仕様によるものです．

  • JAXでJITコンパイルする関数は，基本的にステートレスでないといけない
  • JAXがトレース対象とする変数は，Pythonの制御変数に用いることができない

1つ目の仕様は，関数内でクラス変数などの更新ができないことを示します．
この仕様を満たすために，__call__() に示すようにランダム変数を生成するための self.rng をJIT関数外で更新するようにしています．
また，この仕様はJAXにおけるランダム変数の扱い方にも影響しています．
1つ目の仕様に関する詳細と，JAXにおけるランダム変数の扱いについては，それぞれの公式ドキュメントをご参照ください．

2つ目の仕様は，上のコードでは affine_proc() 内で if val >= self.apply_ratio: というような処理は実装できないことを意味します．
Pythonの if 文はbool型の値を要求するのですが，JITコンパイル時は val や self.apply_ratio，およびそれらの比較はbool型にならずエラーとなるためです．
この仕様を満たすために，affine_proc() では jax.lax.cond() というJIT関数内で使用できる条件分岐を用いて実装しています．

データ拡張処理の実行

必要な処理が実装できましたので，処理を適用してみます．
まず，次のコードで変換クラスをインスタンス化します．

1
2
3
4
5
6
7
8
aug_fn = RandomAffineTransform2D_JAX_JIT(
    center_joints=[11, 12],
    apply_ratio=1.0,
    trans_range=[-100.0, 100.0],
    scale_range=[0.5, 2.0],
    rot_range=[-30.0, 30.0],
    skew_range=[-30.0, 30.0],
    dtype=dtype)

次のコードでは，trackdata (のコピー) に対してランダムなパラメータで変換を施しています．
前項と同じく，1回目の処理呼び出しでは処理のコンパイルが行われるため個別に時間を計測し，2回目以降に同じ処理を複数回適用して平均時間を表示しています．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
testtrack = trackdata.copy()

# The 1st call may be slow because of the computation graph construction.
print(f"Time of first call.")
start = time.perf_counter()
temp = aug_fn(testtrack)
interval = time.perf_counter() - start
print_perf_time(np.array([interval]))

testtrack = trackdata.copy()
print("Time after second call.")
target_fn = partial(aug_fn, inputs=testtrack)
pmeasure(target_fn)

print 処理の結果を示します．
1回目の処理では759.-ミリ秒程度で，2回目以降の処理では654.7マイクロ秒程度でした．
全体をJITコンパイルした場合はかなり高速に動作することが分かります．

Time of first call.
Overall summary: Max 759.034ms, Min 759.034ms, Mean +/- Std 759.034ms +/-   0s
Time after second call.
Overall summary: Max 2.33457ms, Min 648.916µs, Mean +/- Std 727.373µs +/- 231.14µs
Top 10 summary: Max 657.18µs, Min 648.916µs, Mean +/- Std 654.719µs +/- 2.50747µs

入力データ形状が変わった場合の挙動

前項と同じく入力データの形状が変わった場合の挙動を示します．
次のコードは上の変換実行処理とほぼ同じですが，入力データの時間長が1フレーム分短くなっています．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
testtrack = trackdata.copy()

# The 1st call may be slow because of the computation graph construction.
print(f"Time of first call.")
start = time.perf_counter()
temp = aug_fn(testtrack[:-1])
interval = time.perf_counter() - start
print_perf_time(np.array([interval]))

testtrack = trackdata.copy()
print("Time after second call.")
target_fn = partial(aug_fn, inputs=testtrack[:-1])
pmeasure(target_fn)

print 処理の結果を示します．
1回目の処理は729.7ミリ秒程度で，2回目以降の処理では662.4マイクロ秒程度でした．

Time of first call.
Overall summary: Max 729.709ms, Min 729.709ms, Mean +/- Std 729.709ms +/-   0s
Time after second call.
Overall summary: Max 3.6329ms, Min 653.367µs, Mean +/- Std 763.583µs +/- 352.963µs
Top 10 summary: Max 664.35µs, Min 653.367µs, Mean +/- Std 662.35µs +/- 3.05068µs

今回はJAXを用いたアフィン変換処理の実装を試みましたが，如何でしょうか?
現在のJAXは動的な入力や，データの形状や中身に依存して処理ロジックを切り替えることが難しいです．
まだ試していませんが，最大長を想定してJIT関数内部ではマスクを駆使したり，分岐はJIT関数の外でなるべく行うような設計が必要だと感じています．

私もJAXにまだ慣れておらず，色々と勉強中です．
勘違いや誤りがあった場合はご指摘いただけましたら助かります．

今回紹介した話が，動作認識のデータ拡張やJAXの取り扱いなどでお悩みの方に何か参考になれば幸いです．

GPUを使える状態で作ったDockerイメージがいつの間にか動かなくなった
"手話"という語彙が意味するところについて

関連する記事