手話認識入門 補足 - 深掘りTransformer3: 正規化層について

This image is generated with ChatGPT-4 Omni, and edited by the author.
作成日:2024年07月16日(火) 00:00
最終更新日:2024年10月08日(火) 13:10
カテゴリ:手話言語処理
タグ:  手話認識入門 深層学習 正規化層

Transformerの補足説明として，正規化層について説明します．

目次

こんにちは．高山です．
今回は，第九回の記事の補足になります．

手話入門記事の第九回では Transformer-Encoder を用いた孤立手話単語認識を紹介しました．
またこれまでに補足記事の中で，Positional encoding と Multi-head self attention について開設しました．
本記事では，正規化層について説明したいと思います．

Transformer では，主に Layer Normalization が正規化層として用いられていますが，他にも様々な手法が提案されています．
各手法の違いを説明した方が理解がしやすいと思いますので，本記事ではいくつかの有名な手法を取り上げて説明したいと思います．

更新履歴 (大きな変更のみ記載しています)

  • 2024/09/18: カテゴリを変更しました
  • 2024/09/17: タグを更新しました
  • 2024/08/05: 各正規化層の効果，課題に関する表現と説明を更新しました．

1. 正規化層の役割

正規化層ではバッチ内の特徴量から統計量を求め，その統計量を用いて特徴量のスケーリングを行います．
よく用いられる統計量は平均と標準偏差で，下記のような計算を行うことが多いです．

$$ \begin{equation} \label{eqn_normalize} \hat{x} = \frac{x - \mu}{\sigma} \end{equation} $$

式\(\eqref{eqn_normalize}\)において\(x, \mu, \sigma\) は，それぞれ特徴量，平均，標準偏差を示します．
この処理は統計処理において標準化と呼ばれる手法と同様で，変換後の特徴量は平均 0，標準偏差 1 の正規分布 (標準正規分布) に従う値になります．
この処理によって，モデル内部の特徴量スケールが制御され，学習の安定化と収束の高速化を図ることができます．

2. 本記事で紹介する正規化層

通常の統計処理では全データを用いて統計量を算出しますが，Neural network の正規化層ではバッチデータを用いて推論毎に統計量を算出します．
また，統計量をバッチデータの特定の軸に沿って算出することで，それぞれ異なった特性の正規化処理を実装することができます．

本記事で紹介する正規化層を図1に示します．

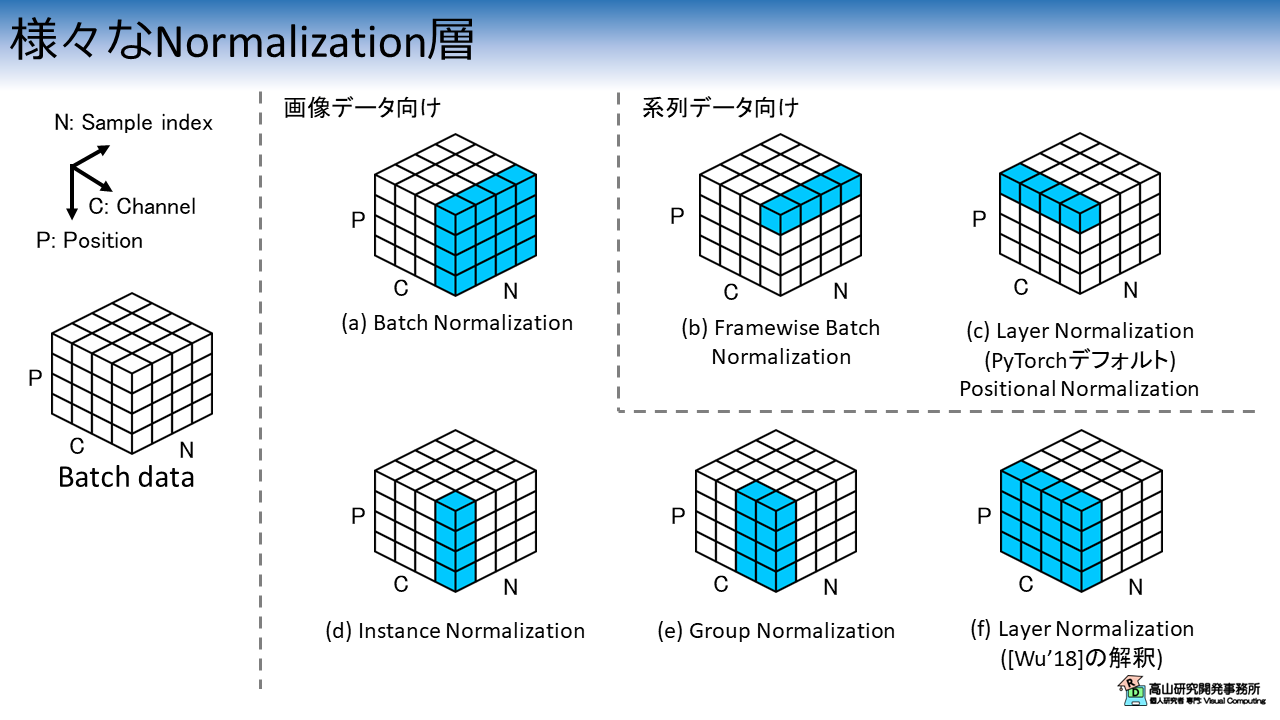
現在広く使われている正規化層を一覧で並べた画像です．各正規化層の正規化軸が色付けされており，手法の特徴が視覚的に分かるように描いています．画像の後に説明があります．
様々な正規化層

立方体 (ボクセルと言います) の配列はバッチデータを示し，各ボクセルは特徴量を示します．
ボクセルは下記に示すN, C, P の3軸に沿って並んでいます．

  • N: バッチ内のサンプルインデクス
  • C: 特徴次元インデクス
  • P: 空間や時間インデクス

画像データなどの場合は，P軸は2次元インデクスで表すこともできます．

図1で青塗りされているボクセルは，統計量を算出する軸を示します．
例えば，図1(a) の Batch Normalization の場合は，P軸と N軸に沿って統計量を算出します．
(つまり，C のインデクス値毎に異なる統計量が算出されます)

統計量を算出する際にどの軸を用いるかによって正規化の特性が変わります．
特に，P軸を統計量算出軸から除外した手法は，系列データ向けに提案されている場合が多いです．
今回は，下記に示す手法を紹介していきます．

  • 図1(a) Batch Normalization (BN) [Ioffe'15]: P軸，N軸
  • 図1(b) Framewise Batch Normalization (FBN) [Laurent'15]: N軸
  • 図1(c) Layer Normalization (LB) [Ba'16]: C軸
  • 図1(d) Instance Normalization (IB) [Ulyanov'17]: P軸
  • 図1(e) Layer Normalization by Wu [Wu'18]: P軸，C軸
  • 図1(f) Group Normalization [Wu'18]: P軸，(グループ分けした) C軸

  • [Ioffe'15]: S. Ioffe, et al., "Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift," Proc. of the ICML, available here, 2015.
  • [Laurent'15]: C. Laurent, et al., "Batch normalized recurrent neural networks," Proc. of the ICASSP, available here, 2016.
  • [Ba'16]: J. Ba, et al., "Layer Normalization," arXiV: 1607.06450, available here, 2016.
  • [Ulyanov'17]: D. Ulyanov, et al., "Instance Normalization: The Missing Ingredient for Fast Stylization," arXiV: 1607.08022, available here, 2017.
  • [Wu'18]: Y. Wu, et al., "Group Normalization," Proc. of the ECCV, available here, 2018.

3. 正規化層の計算手順

今回紹介する正規化手法は統計量を算出する軸がそれぞれ異なっていますが，基本的な計算手順は同様ですので，最初に定式化を行いたいと思います． (ここでは文献[Wu'18]の表現を借りて説明します．気になる方は原著をご参照ください)

正規化層では，次の式を用いて特徴量をスケーリングします．

$$ \begin{equation} \hat{x}_{i} = \frac{1}{\sigma_i} (x_{i} + \mu_{i}) \end{equation} $$

\(i=(i_{N}, i_{C}, i_{P})\) は各軸に沿ったバッチ内の特徴量インデクスを示します．
平均値 \(\mu_i\) と標準偏差 \(\sigma_{i}\) は次の式で求めます．

$$ \begin{eqnarray} \label{eqn_general_form} \mu_{i} = \frac{1}{m} \sum_{k \in S_i} x_k \\ \sigma_{i} = \sqrt{ \frac{1}{m} \sum_{k \in S_i} (x_k - \mu_i)^2 + \epsilon } \end{eqnarray} $$

\(\epsilon\) はゼロ除算を避けるための微小変数です．
\(S_i\) は統計量算出軸に沿ったインデクス集合で，各正規化層は \(S_i\) によって定義されます．
\(m\) はインデクス集合のサイズを示します．

正規化層では，この後学習パラメータ \(\gamma\) と \(\beta\) を用いて次の式で線形変換を行います．

$$ \begin{equation} \label{eqn_affine} y_{i} = \gamma \hat{x}_i + \beta \end{equation} $$

なお，\(\gamma\) と \(\beta\) は 特徴次元のと同サイズのベクトルで，式\(\eqref{eqn_affine}\) はチャネル毎に計算します．
上記の処理によって変換後の分布にバリエーションを持たせる (標準正規分布に限定されない) ことができるようになり，特徴抽出の性能が保てるようになります．

次節以降では，各正規化手法を一つずつ紹介していきます．

4. Batch Normalization

図2に BN の特性を示します．

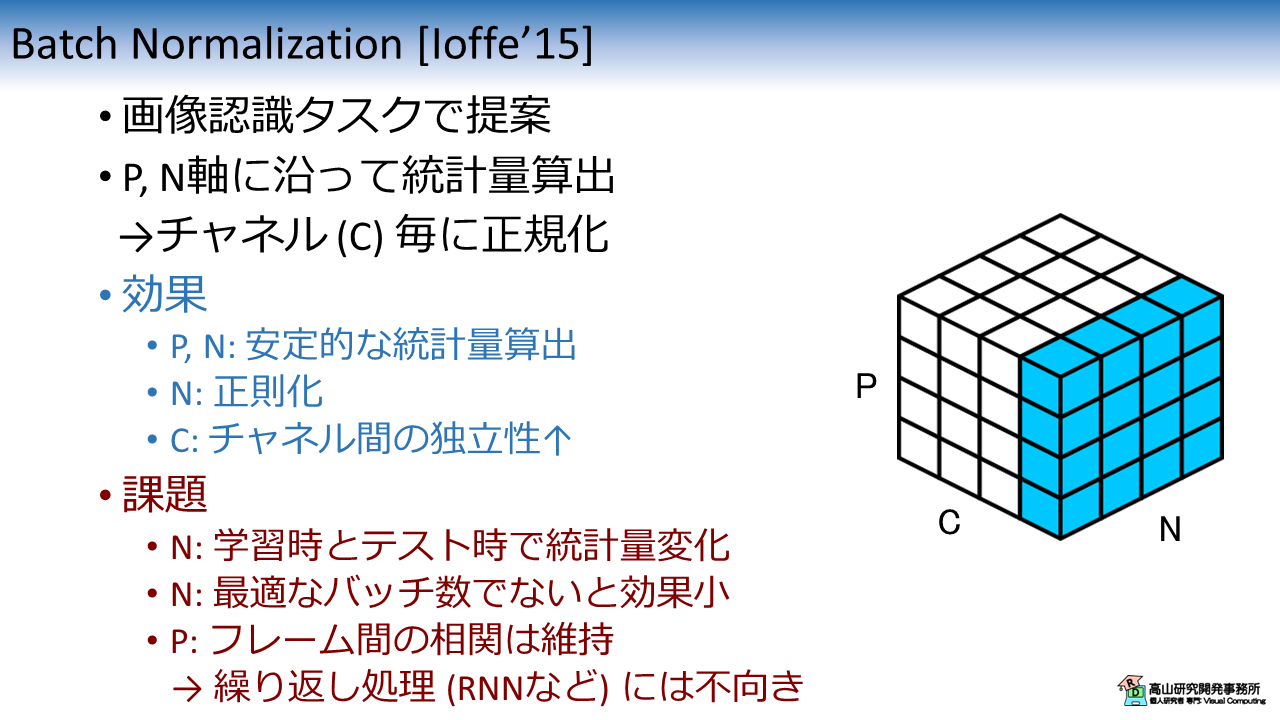
Batch Normalizationの特徴を説明する画像です．画像の後に説明があります．
Batch Normalization [Ioffe'15]

BN は最初期に提案された正規化層で，最も有名な手法と言えるでしょう．
当初は画像認識タスク向けに提案されましたが，現在では様々なタスクで使われています．

BNでは，P軸とN軸に沿って統計量を算出し，チャネル毎に正規化を行います．
式\(\eqref{eqn_general_form}\) のインデクス集合 \(S_i\) は下記のように表せます．

$$ \begin{equation} S_i = \{k \ | \ k_C = i_C\} \end{equation} $$

BN は P軸と N軸を統計量算出軸に含むことから，統計算出が安定しやすいです．
また，チャネル毎に異なる値で正規化を行うため，チャネル間の独立性が向上しやすいです．
さらに，N軸は学習時にランダムサンプリングが行われるため，正則化の効果があると言われています．

テスト時はバッチデータを形成できないことから，BNでは学習時の統計量を用いて推論を行います．
そのため，テストデータの統計量が学習時と大きく異なる場合に，アジャストできないという課題があります．

また，バッチ数が小さいと正規化が安定せず，大き過ぎると正則化の効果が弱まることから，最適なバッチ数を決定する必要があります．

さらに，P軸を統計量算出軸に含んでいることから，フレーム間の相関などサンプル内の相対的な関係は維持されます．
そのため， RNN などの繰り返し処理では正規化の効果が弱まる場合があります．

5. Framewise Batch Normalization

図3に FBN の特性を示します．

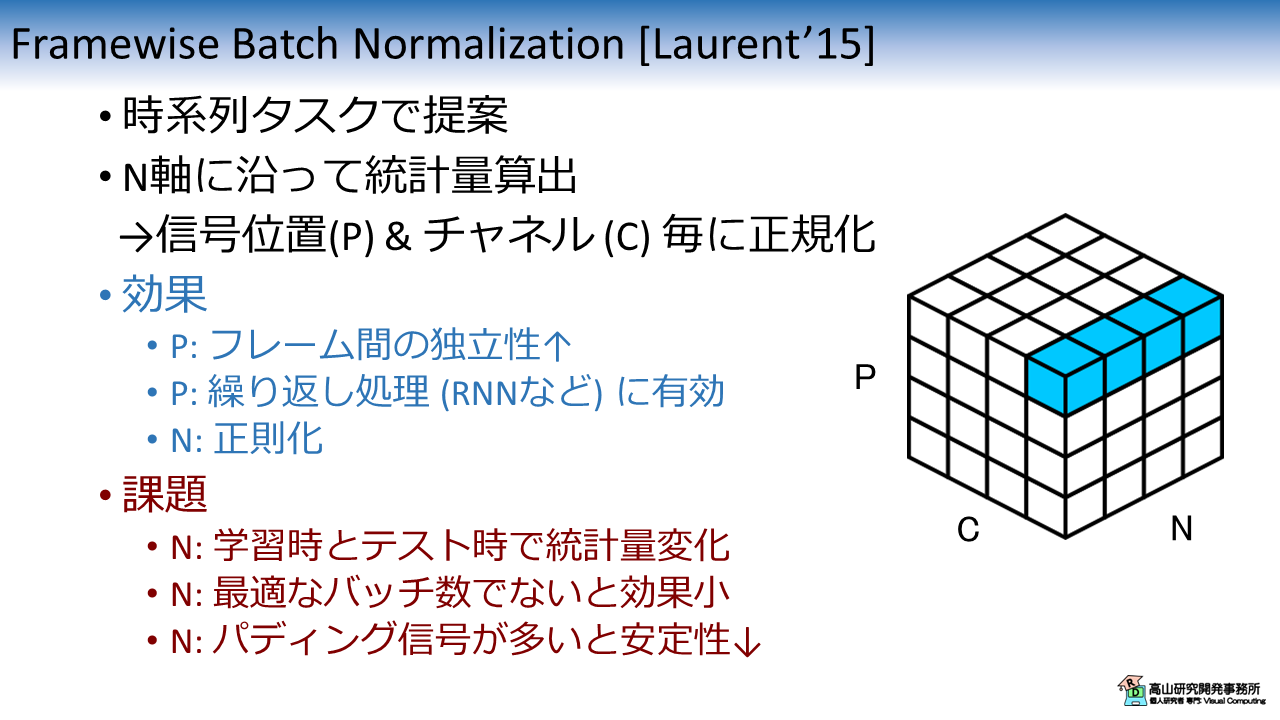
Framewise Batch Normalizationの特徴を説明する画像です．画像の後に説明があります．
Framewise Batch Normalization [Laurent'15]

FBN は BN を Recurrent Neural Network (RNN) に適用するために改良した手法です．
N軸に沿って統計量を算出し，信号位置とチャネル毎に正規化を行います．
式\(\eqref{eqn_general_form}\) のインデクス集合 \(S_i\) は下記のように表せます．

$$ \begin{equation} S_i = \{k \ | \ k_C = i_C, k_P = i_P \} \end{equation} $$

系列データは隣接フレーム間で似た特徴量を持つ場合が多く相関が高いです．
そのため，RNN などの繰り返し処理では学習効率が落ちる場合があります． FBN では，P軸を統計量算出軸から除外することで (各フレームを異なる値で正規化することで)，フレーム間の独立性を高めてこの問題に対処しています．

ただし，N軸を基に統計量を算出することから，パディングデータを含んでいる場合は統計量算出が不安定になる課題があります．

6. Layer Normalization

図4に LN の特性を示します．

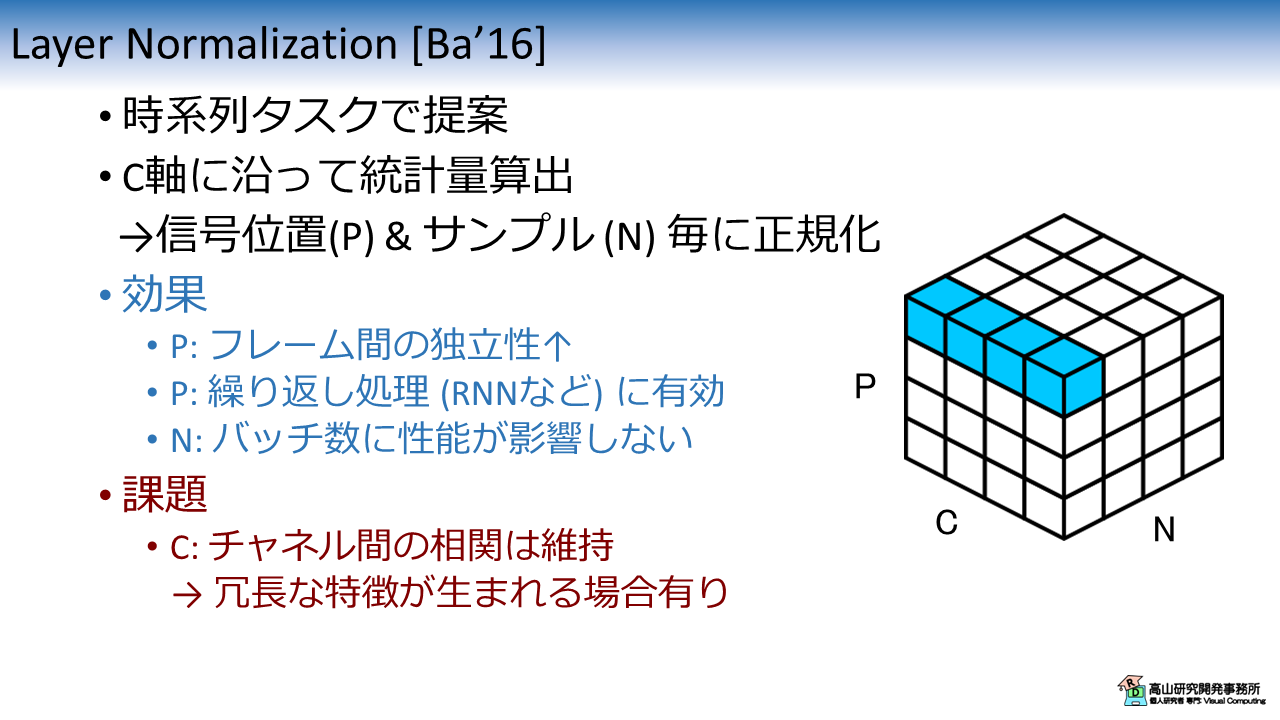
Layer Normalizationの特徴を説明する画像です．画像の後に説明があります．
Layer Normalization [Ba'16]

LN は FBN と同様に，RNN に対して正規化を行うために提案されました．
Transformer [Vaswani'17] に採用されてから知名度が上がり，系列データに対する正規化処理のスタンダードになっています．

LN は C軸に沿って統計量を算出し，信号位置とサンプル毎に正規化を行います．
式\(\eqref{eqn_general_form}\) のインデクス集合 \(S_i\) は下記のように表せます．

$$ \begin{equation} S_i = \{k \ | \ k_N = i_N, k_P = i_P \} \end{equation} $$

FBN と同様に，LN も P軸を統計量算出軸から除外することでRNNなどの繰り返し処理に適用可能にしています．
また，FBN と異なり N軸を統計量算出に用いていないことから，パディング信号の影響を受けません．

一方，C軸を基に統計量を算出していることから，チャネル間の相関は維持されます．
そのため，相関が高いチャネルが存在すると冗長な特徴量が増えて認識性能向上への効果が弱まると考えられます．
また，(実験は見当たりませんでしたが) チャネル数が少ないと統計量算出が不安定になることも予想されます．

  • [Vaswani'17]: A. Vaswani, et al., "Attention is all you need," Proc. of the NIPS, available here, 2017.

7. Instance Normalization

図5に IN の特性を示します．

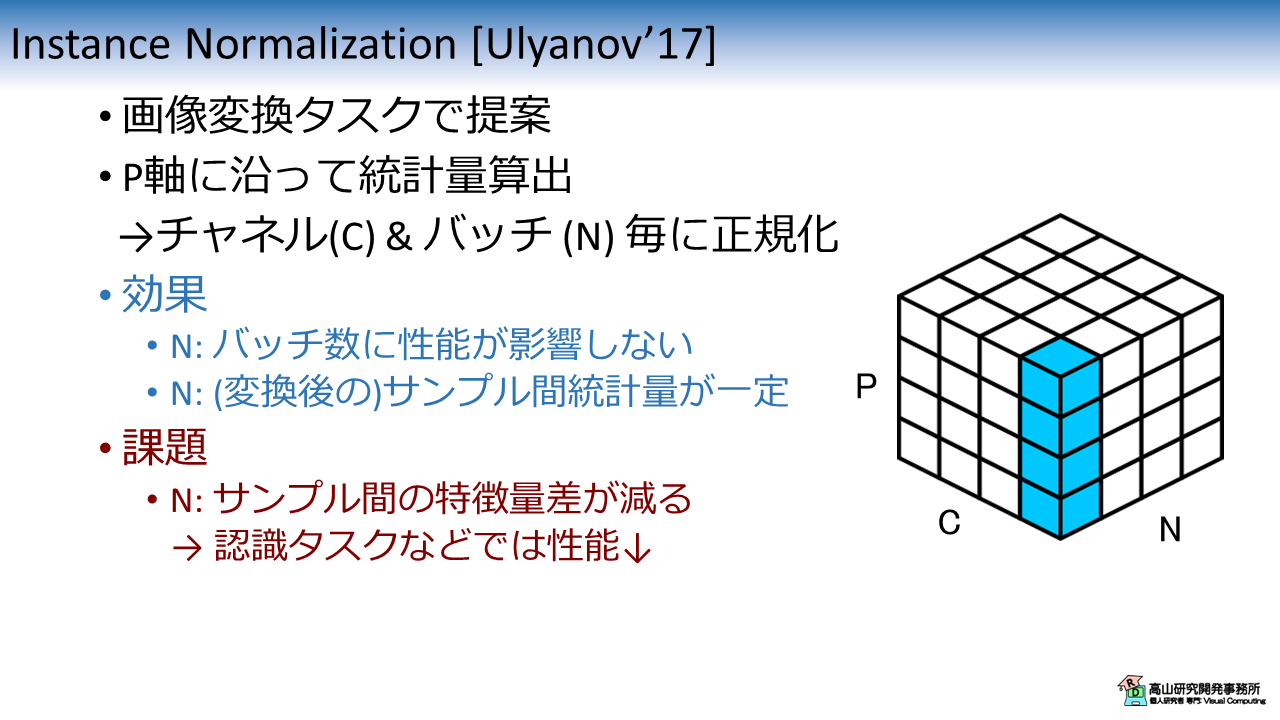
Instance Normalizationの特徴を説明する画像です．画像の後に説明があります．
Instance Normalization [Ulyanov'17]

IN は画像変換タスクに対して正規化を行うために提案されました．

IN は P軸に沿って統計量を算出し，チャネルとバッチ毎に正規化を行います．
式\(\eqref{eqn_general_form}\) のインデクス集合 \(S_i\) は下記のように表せます．

$$ \begin{equation} S_i = \{k \ | \ k_N = i_N, k_C = i_C \} \end{equation} $$

このタスクでは，変換前画像のエッジなどは維持しながら，明暗などの特徴は正規化したい (無個性化したい) という要求があります．
BN のように N軸を統計量算出に用いて正規化をすると，バッチ内の相対的な特徴差が維持されてしまいます．
IN では N軸を統計量算出軸から除外することでこの問題に対処しています．

ただしこの処理はサンプル間の特徴量差が減ることに繋がるので，認識タスクなどでは性能が劣化する場合が多いです．

8. Layer Normalization (Wuらの手法)

図6は文献[Wu'18] で紹介されている LN の特性を示します．

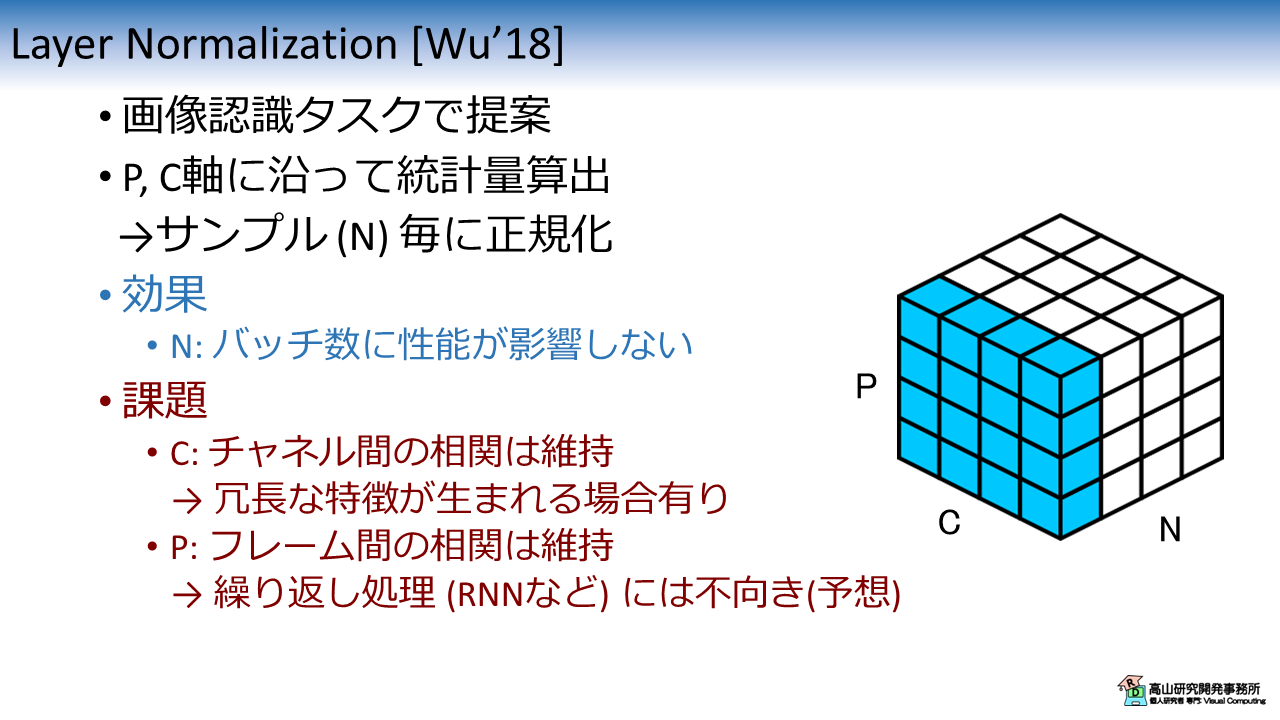
WuらのLayer Normalizationの特徴を説明する画像です．画像の後に説明があります．
Layer Normalization [Wu'18]

この手法は文献[Wu'18] において GN との比較のために用いられた手法です．
LN [Wu'18] は LN [Ba'16] を画像認識タスク向けに改良した手法と言えますが，文献[Wu'18] では明確に区別されていないようです．
その結果，少し誤解された情報が広まっているように感じています (特に，正規化の比較図)．

例えばこちらのIssueでは，PyTorch の実装と文献[Wu'18] との不整合が指摘されていますが，PyTorchの LN 実装は (デフォルト設定では) 文献[Ba'16] に基づいており，文献[Wu'18] の方が LN の亜種であると思っています (個人的感想です)．

LN [Wu'18] は P軸と C軸に沿って統計量を算出し，サンプル毎に正規化を行います．
式\(\eqref{eqn_general_form}\) のインデクス集合 \(S_i\) は下記のように表せます．

$$ \begin{equation} S_i = \{k \ | \ k_N = i_N \} \end{equation} $$

N軸が統計量算出軸から除外されていることから LN [Ba'16] と同様に，バッチ数に性能が影響されない特性があります．

一方，C軸を基に統計量を算出していることから，チャネル間の相関が高いと認識性能向上への効果が弱まると考えられます．
また，P軸を統計量算出軸に用いていることから，(文献[Wu'18]の主張とは異なり) RNN などの繰り返し処理には不向きではと感じています (高山の個人的予想です)．

9. Group Normalization

図7に GN の特性を示します．

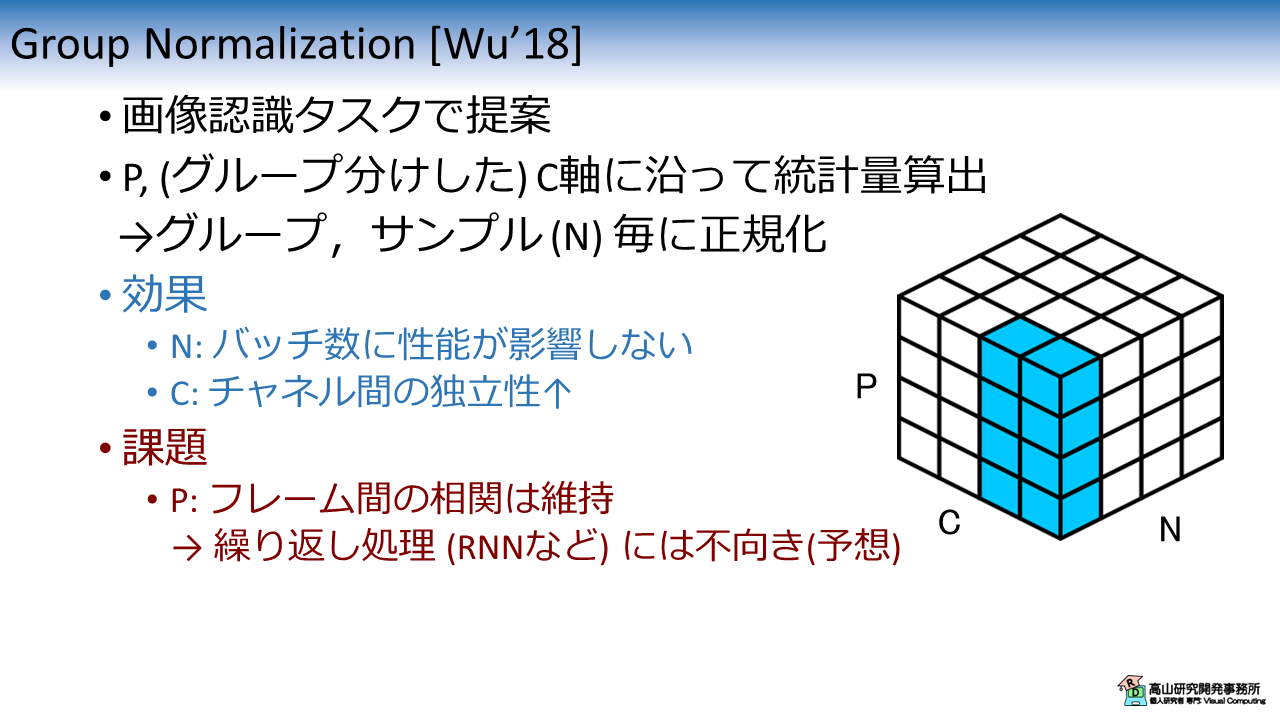
Group Normalizationの特徴を説明する画像です．画像の後に説明があります．
Group Normalization [Wu'18]

GN は LN [Wu'18] で抱えていたチャネル間の相関問題に対処するために提案された手法です．
この手法ではチャネルを予めグループ分けし，P軸およびグループ分けした C軸に沿って統計量を算出します．
式\(\eqref{eqn_general_form}\) のインデクス集合 \(S_i\) は下記のように表せます．

$$ \begin{equation} S_i = \{k \ | \ k_N = i_N, \lfloor \frac{k_C}{C/G} \rfloor = \lfloor \frac{i_C}{C/G} \rfloor \} \end{equation} $$

\(G, C/G\) は，それぞれグループ数と1グループあたりのチャネル数を示します．
\(\lfloor \cdot \rfloor\) は引数以下の最大整数を返す，床関数を示します．

LN [Wu'18] ではチャネル間の相関が問題になっていましたが，チャネルを予めグループ分けすることで影響を緩和することができます．

一方で，P軸を統計量算出軸に用いていることから，(文献[Wu'18]の主張とは異なり) RNN などの繰り返し処理には不向きであると予想されます．
ではP軸を除外すれば良いかと言うと，GNの場合はチャネルが分割されていることから統計量算出に用いる特徴量数が少なくなり，統計量算出が不安定になるのではと感じています (こちらも個人的予想です)．
中々難しい問題ですね(^^;)．

10. まとめ

最後にまとめとして，バッチデータと統計量を算出する軸の関係を図8に示します．

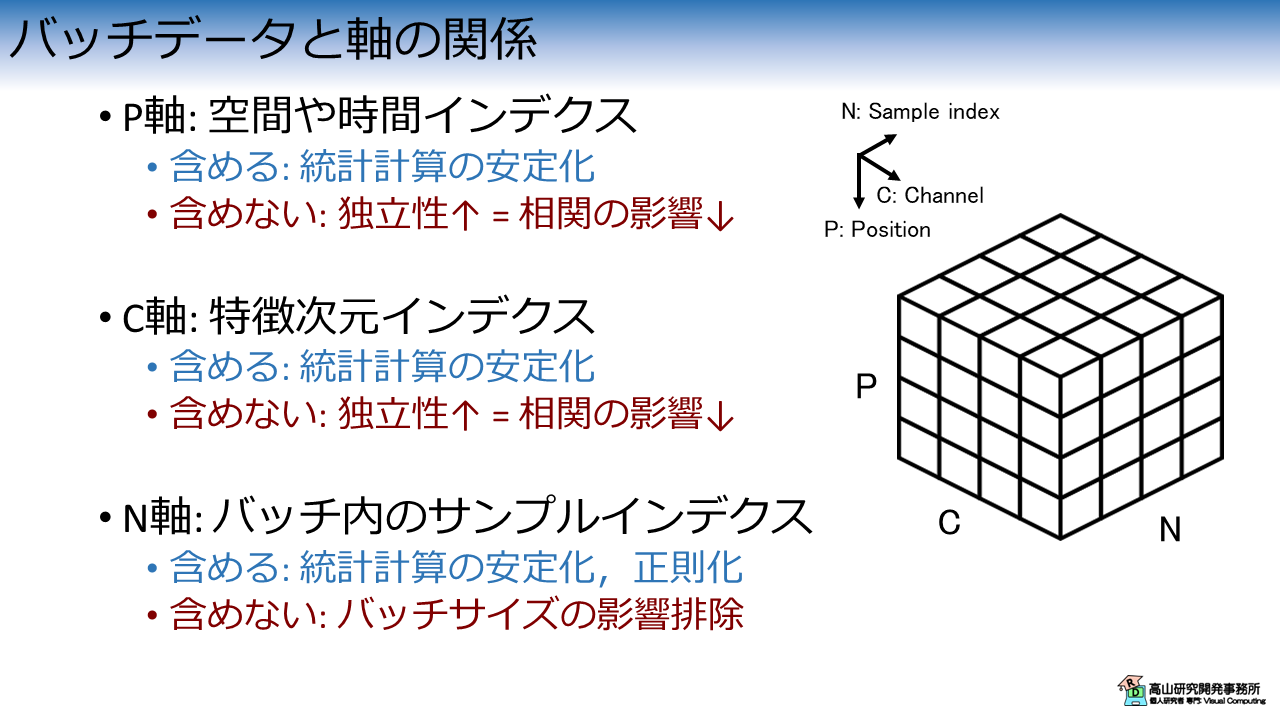
バッチデータと軸の関係を整理して説明した画像です．画像の後に説明があります．
バッチデータと軸の関係

基本的に，統計量算出軸を多く含めると，統計計算は安定しやすくなります．
一方で，特定の軸に沿った相対的な関係 (相関など) は維持されますので，そこが問題になる場合は性能が上がりにくくなります．

N軸は他の軸とは少し捉え方が異なります．
学習時はデータをランダムサンプリングしてパッチデータを形成することが多いです．
そのため，サンプル間の相関が問題になることは無いようです．
また，N軸に沿って統計量を算出した場合は，ランダムサンプリングによる正則化効果があると言われています．

一方で，学習時とテスト時ではバッチ内のサンプル数が異なることから，N軸に沿って統計量を算出する場合はバッチサイズの影響を受けやすくなることが知られています．

統計量算出軸の設定によって様々な正規化手法を実装できますが，各手法の長所と短所は表裏一体になっていることが分かります．
目的に沿って適切な正規化処理を選択することが重要ですね．

今回は 比較的有名な正規化層について紹介しましたが，如何でしたでしょうか?
LN [Ba'16] と LN [Wu'18] の違いについては以前から気になっており，やっと記事にすることができてスッキリしました(^^)．

今回は統計量算出軸の違いに焦点を絞って紹介しましたが，他にも正規化層の組み合わせ [Luo'19]，統計量の変更 [Shen'20]，BN におけるパディング信号のマスキング [Takayama'21] (手前味噌ですみません(^^;)) など様々な改良が成されています．

今後も様々な手法が提案されていくと思いますので，追っていくと面白い発見がありそうですね．

今回紹介した話が，これから手話認識や深層学習を勉強してみようとお考えの方に何か参考になれば幸いです．

  • [Luo'19]: P. Luo, et al., "Switchable Normalization for Learning-to-Normalize Deep Representation," IEEE Trans. on PAMI., available here, 2019.
  • [Shen'20]: S. Shen, et al., "PowerNorm: Rethinking Batch Normalization in Transformers," Proc. of the ICML, available here, 2020.
  • [Takayama'21]: N. Takayama, et al., "Masked Batch Normalization to Improve Tracking-Based Sign Language Recognition Using Graph Convolutional Networks," Proc. of the FG, 2021.
手話認識入門17 - 様々な改善手法8: 時系列リサイジングによる処理軽量化
手話認識入門 補足 - 深掘りTransformer4: 欠損値の補間は認識性能を向上させるのか?

関連する記事