こんにちは．高山です．
今回は，第九回の記事の補足になります．

手話入門記事の第九回では Transformer-Encoder を用いた孤立手話単語認識を紹介しました．
このときの記事では実装を中心として説明し，各処理モジュールについては細かく説明していませんでしたので，本記事で補足説明をさせていただきたいと思います．

Transformer は下記の処理モジュールから構成されています．
(Residual connection は処理モジュールというよりはネットワーク設計技術というような立ち位置です)

• Positional encoding
• Multi-head (self-) attention
• Position-wise feed forward network
• Layer normalization
• Residual connection

全てを一度に紹介するとかなり長文になってしまいそうなので，今回は Positional encoding (PE) に焦点を絞って説明させていただきたいと思います．
他の処理モジュールについてはまた別記事で紹介します．

更新履歴 (大きな変更のみ記載しています)

• 2024/09/18: カテゴリを変更しました
• 2024/09/17: タグを更新しました

1. 認識モデルと Positional encoding の関係

まず最初に，孤立単語認識モデルとPE 層の関係についておさらいしたいと思います．

図1は，孤立単語認識モデルと Transformer-Encoder ブロック，そして PE 層の関係を示しています．

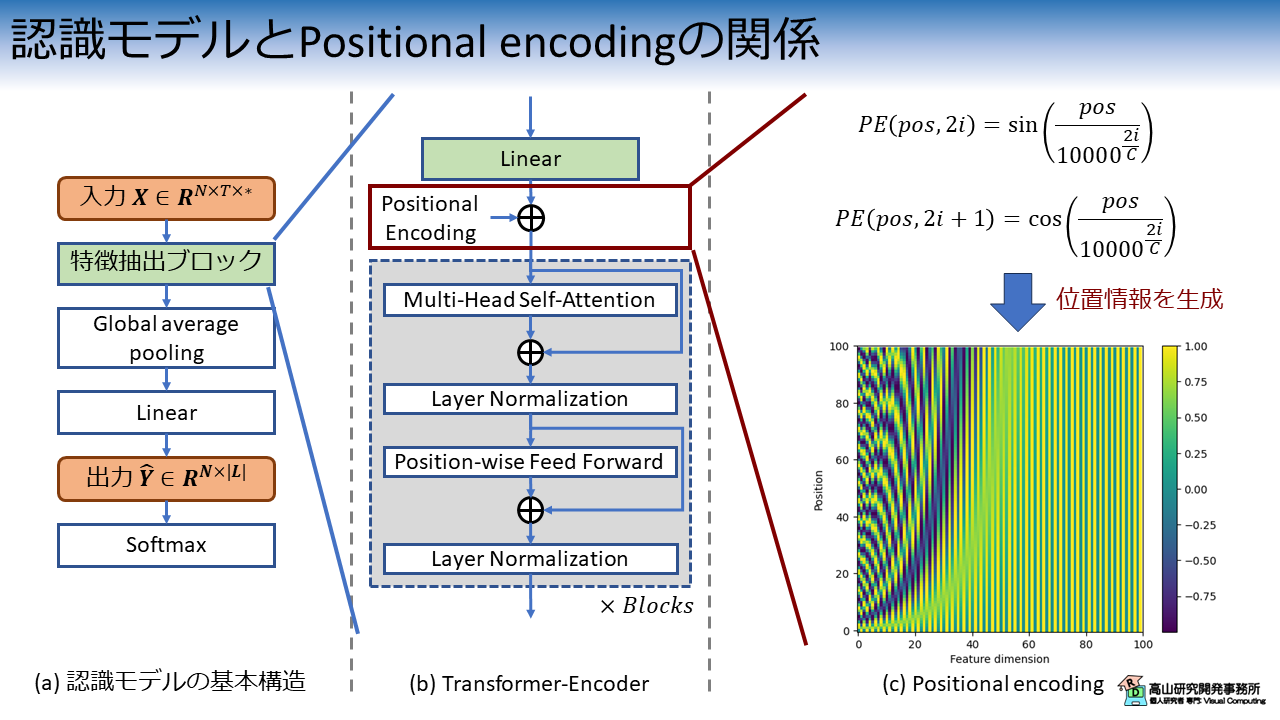
Transformer-Encoder ブロックは認識モデルの特徴抽出ブロックとして配置され，PE 層は Transformer-Encoder ブロックの手前に配置されます．

Transformer には，入力データの位置関係を処理する層がありません．
(RNN の場合は，繰り返し処理によって "あるフレームが別のフレームよりも後" といった情報を取り扱っています)
PE はこの問題に対処するための技術で，図1(c) に示すように三角関数を用いた位置信号を生成します．

位置信号の生成においては，下記の2点の要求を満たす必要があります．

• 位置毎にユニークな信号を生成
• 位置信号の値が一定の範囲に収まっている

続く節では，これらの点についてもう少し深堀りして説明していきたいと思います．

2. 多種類の三角関数によるユニークな位置情報の生成

PE 層の位置信号は次の式に従って生成されます．

式 \(\eqref{eqn_pe_sin}\) は偶数番目の特徴量次元に対応する位置信号を示し，式 \(\eqref{eqn_pe_cos}\) は奇数番目の特徴量次元に対応する位置信号を示します．
\(C\) は入力特徴量の次元数を示し，\(10000\) はユーザが指定するパラメータです．

式 \(\eqref{eqn_pe_sin}\), \(\eqref{eqn_pe_cos}\) に示されるとおり，PE層は多種類の三角関数を用いて多次元の位置信号を生成します．
この処理がどのような意味を持つかをイメージするために，まず1種類の三角関数を用いて位置信号を生成した場合を考えてみます．

2.1 1種類の三角関数を用いた場合

図2は，1種類の三角関数で位置信号を与えた場合のグラフを示しています．

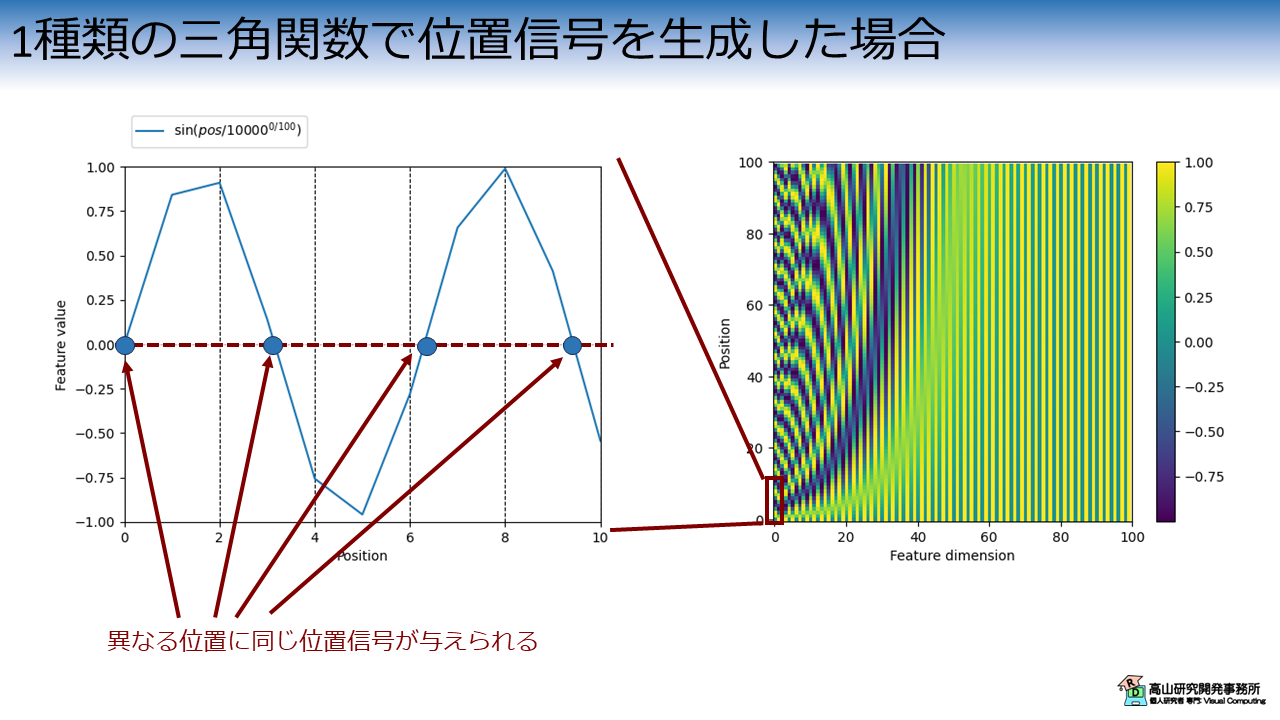
図2左側のグラフでは，縦軸は位置信号の値を示し，横軸は位置 (手話認識の場合は時間) を示します．
PE層が本来出力する信号に対しては，赤枠で囲まれた部分が図2左側のグラフに対応します．

三角関数は周期関数であるため，異なる位置に同じ位置信号が与えられます．
(生の出力をそのままプロットしたため離散信号になっていますが，連続信号として説明しています)
入力信号の位置関係が重要なタスクの場合，この処理では位置関係を適切に捉えられないため性能が下がってしまう恐れがあります．

2.2 多種類の三角関数を用いた場合

では図3に示すように，多種類の三角関数を用いて位置信号を与えた場合はどうでしょうか．

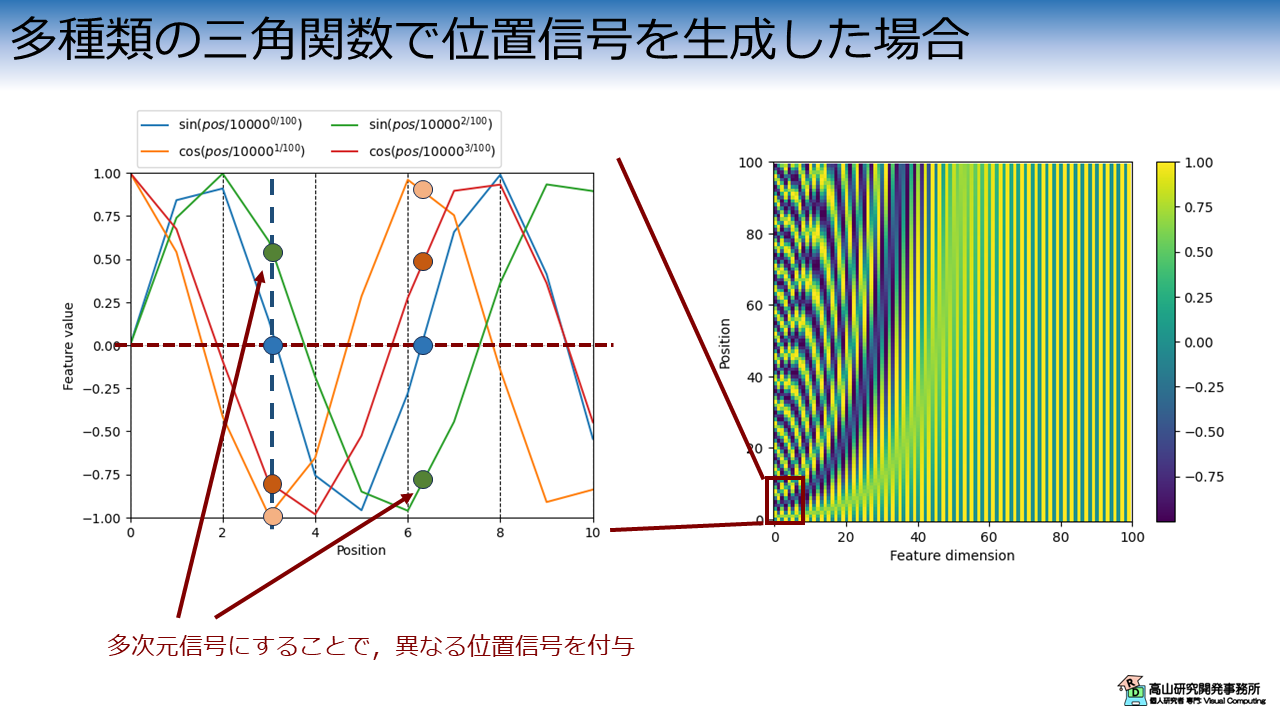
図3左側のグラフに示すとおり，PE層は特徴量次元毎に波長の異なる三角関数を用いて位置信号を生成します．
この場合，ある波長の三角関数では同じ値 (青丸) になったとしても，他の波長の三角関数では異なる値 (他の色の丸) になります．
モデルは異なる値となる位置信号を手がかりとして，入力信号の位置関係を捉えることが可能になります．

特徴量次元は数十から数百など大きな値であることが多いため，多種類の三角関数を用いてユニークな位置信号を生成することが可能になります．

3. 位置信号のスケールと特徴量の関係

次に，位置信号の値が一定の範囲に収まっている効果について説明します．

図1(b) に示したように，PE 層は入力特徴量に位置信号を加算することで位置情報を付加します．
そのため，入力特徴量に対して位置信号のスケールが大きい場合は入力特徴量が大きく変化してしまいます．

図4に，位置信号のスケールに応じて，位置信号加算後の特徴量がどのように変化するかを示します．

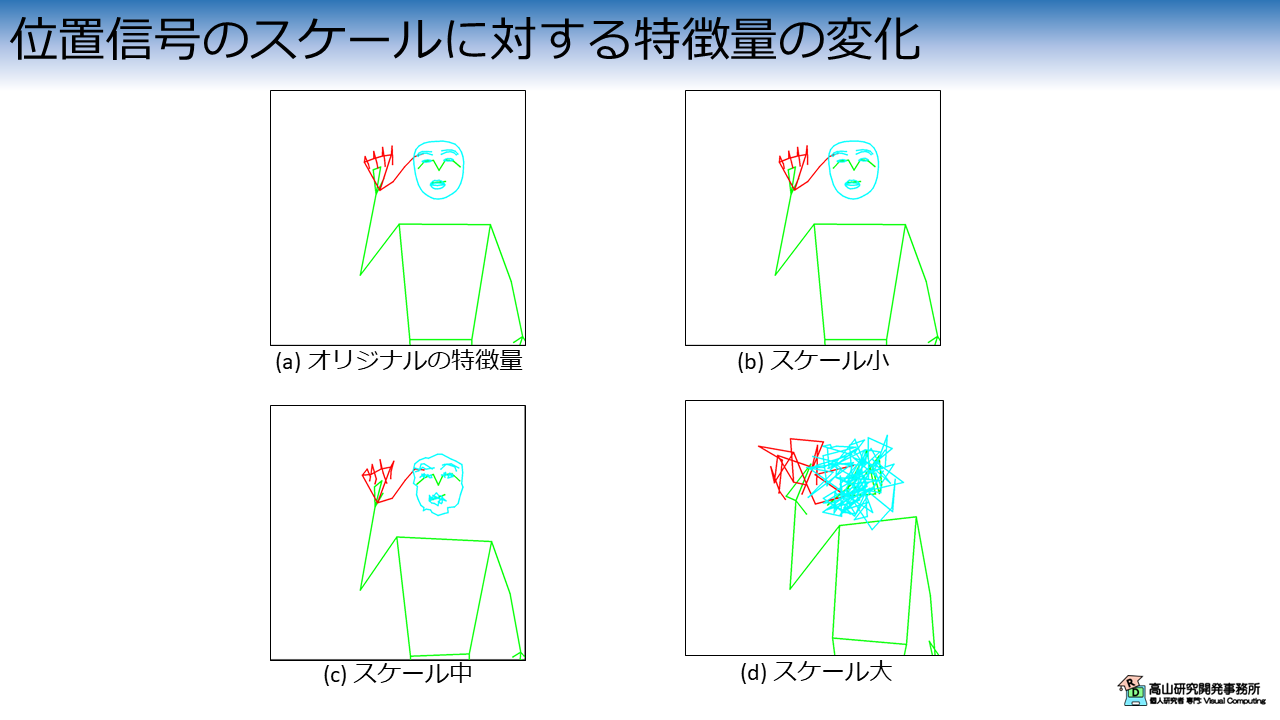
図4では単純に生の追跡点座標 (指文字の"あ"を表出しています) を入力特徴量として，ランダムに生成した位置信号を加算しています．
図4(a) はオリジナルの特徴量を示し，図4(b) から (d) でスケールの異なる位置信号を加算した結果を示しています．

位置信号のスケールが小さい場合は，入力特徴量が示している情報に大きな変化はありません． スケールが大きくなるにつれてオリジナルの情報が崩れていき，図4(d) に示すケースでは元の指文字が何だったのかを読み取るのは難しくなってしまっています．

このように，位置信号のスケールが固定されていることは入力特徴量が持つ情報を保持するために重要です．
PE 層は三角関数に基づいて位置信号を生成するため，出力値は \([-1, 1]\) の範囲になり，この要求を満たすことができます．

今回は Positional encoding の動作，特徴について少し細かく紹介しましたが，如何でしたでしょうか?

Positional encoding は何と言っても事前計算可能で，推論時はメモリアクセスで位置信号が取り出せるな点が秀逸ですね．
改めてよくできた手法だなと思いました．

位置情報を付加する (場合によっては他のモジュールで代替することで削除する) 手法は現在でも検討が続いています[Shaw'18, Huang'20, Liu'21, Wu'21-1, Wu'21-2, Chu'23]．
タスクの特性 (相対的な位置が重要，入力が2次元画像など) を活かす工夫も多く提案されている印象です．
深く追っていくと改善のヒントが見つかるかもしれませんね．

今回紹介した話が，これから手話認識や深層学習を勉強してみようとお考えの方に何か参考になれば幸いです．

• [Shaw'18]: P. Shaw et al., "Self-Attention with Relative Position Representations," Proc. of the NAACL-HLT, available here, 2018.
• [Huang'20]: Z. Huang et al., "Improve Transformer Models with Better Relative Position Embeddings," Proc. of the EMNLP, available here, 2020.
• [Liu'21]: Z. Liu et al., "Swin Transformer: Hierarchical Vision Transformer using Shifted Windows," Proc. of the ICCV, available here, 2021.
• [Wu'21-1]: K. Wu et al., "Rethinking and Improving Relative Position Encoding for Vision Transformer," Proc. of the ICCV, available here, 2021.
• [Wu'21-2]: H. Wu et al., "CvT: Introducing Convolutions to Vision Transformers," Proc. of the ICCV, available here, 2021.
• [Chu'23]: X. Chu et al., "Conditional Positional Encodings for Vision Transformers," Proc. of the ICLR, available here, 2023.