こんにちは．高山です．
今回は，第九回の記事の補足になります．

手話入門記事の第九回では Transformer-Encoder を用いた孤立手話単語認識を紹介しました．
また前回の記事では，Positional encoding の動作について解説しました．
本記事では，Multi-head self attention (MHSA) の動作について説明したいと思います．

更新履歴 (大きな変更のみ記載しています)

• 2024/09/18: カテゴリを変更しました
• 2024/09/17: タグを更新しました
• 2024/09/04: Location-aware attention の説明に誤りがあったため，訂正しました．

1. 認識モデルと Multi-head self-attention の関係

まず最初に，孤立単語認識モデルとMHSA 層の関係についておさらいしたいと思います．

図1は，孤立単語認識モデルと Transformer-Encoder ブロック，そして MHSA 層の関係を示しています．

Transformer-Encoder ブロックは認識モデルの特徴抽出ブロックとして配置され，MHSA 層は各 Transformer-Encoder ブロックの最初に配置されます．

MHSAでは，Scaled dot-product attention，および Multi-head 処理と呼ぶ技術が提案されています[Vaswani'17]．

Scaled dot-product attention は， Attention と呼ばれる重み行列を内部で生成する技術です．
Transformer では Attention を利用して入力系列のフレーム間の関係性を捉えながら特徴抽出を行います．
Attention 自体は以前から提案されており，Scaled dot-product attention は文献[Luong'15]で提案された Dot-product attention を改良した手法になっています．

Multi-head 処理は，特徴次元軸に沿って特徴量を予めグループ化し，各グループで独立に処理を行うことで相補的な効果を狙う技術です．

両方の技術を同時に説明すると分かりにくいと思いますので，まず次節では Attention の発展の経緯を追っていきながら，Scaled dot-product attention について説明したいと思います．
続く第3節では，MHSAの各処理を Step by step で説明していきながら Multi-head 処理を説明したいと思います．

• [Luong'15]: M.-T. Luong, et al., "Effective Approaches to Attention-based Neural Machine Translation," Proc. of the EMNLP, available here, 2015.
• [Vaswani'17]: A. Vaswani, et al., "Attention Is All You Need," Proc. of the NIPS, available here, 2017.

2. Attentionの発展

入力の重要な部分に重み付けをして処理をする，というアイデア自体は深層学習が流行る以前から取り組まれています．
(例えば，画像処理の分野などでは顕著性マップ[Itti'98]が知られています)
Transformerに繋がる流れの中では，文献[Bahdanau'15]と文献[Luong'15]の手法が特に有名ですので，本節ではこれらの手法を簡単に紹介したいと思います．

• [Itti'98]: L. Itti, et al., "A Model of Saliency-based Visual Attention for Rapid Scene Analysys," IEEE Trans. PAMI, pp.1254-1259, available here, 1998.
• [Bahdanau'15]: D. Bahdanau, et al., "Neural Machine Translation by Jointly Learning to Align and Translate," Proc. of the ICLR, available here, 2015.
• [Luong'15]: M.-T. Luong, et al., "Effective Approaches to Attention-based Neural Machine Translation," Proc. of the EMNLP, available here, 2015.

2.1 Bahdanau RNN with Attention

文献[Bahdanau'15]では，自然言語の翻訳タスク (フランス語から英語など) に取り組んでいて，Recurrent neural network (RNN) ベースの翻訳モデルが提案されています．
高山の知る限りでは，翻訳タスクに Attention が取り入れられたのはこの文献が初めてで，以後 Attention は深層学習の重要技術の一つになっていきます．

図2に文献[Bahdanau'15]で提案しているモデルの処理構成を示します．
(Attentionに関わる部分のみ記載しています．実際はもう少し複雑です)

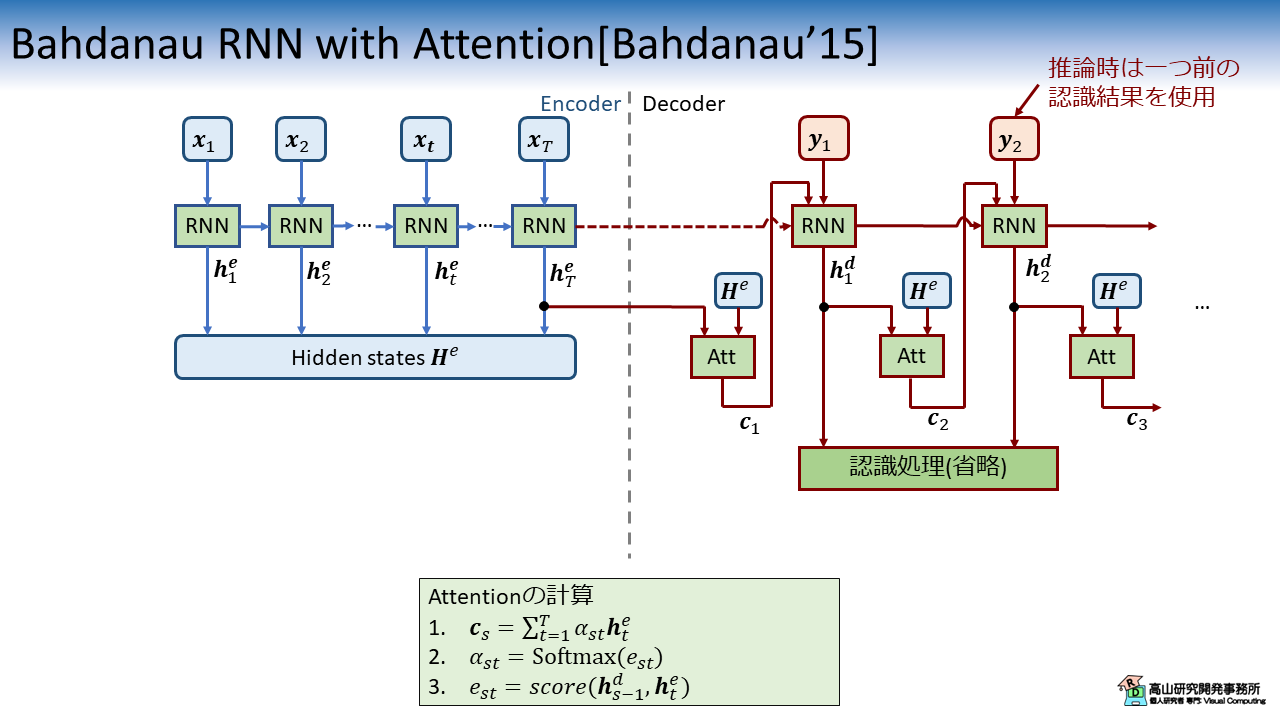
文献[Bahdanau'15]で提案されたモデルは，Encoder-Decoder モデル (Sequence 2 sequence モデルとも呼ばれます) というタイプのモデルです．
このタイプのモデルでは，2種類の系列をEncoder と Decoderにそれぞれ入力して，一方の系列から他方の系列へ変換する処理を行います．

Encoder では RNN を使用して入力系列 \(\boldsymbol{x}_t\) の特徴変換を行います．
変換後の特徴系列 \(\boldsymbol{H}^e = \{\boldsymbol{h}^e_t | 1 \leq t \leq T\}\) は Attention 層へ入力されます．

Decoder では RNN を使用して現在の入力データ \(\boldsymbol{y}_s\) から次のデータ \(\boldsymbol{y}_{s+1}\) を予測します．
Attention 層はこのとき，Encoder の特徴系列 \(\boldsymbol{H}^e\) と一つ前の Decoder-RNN の出力 \(\boldsymbol{h}^d_{s-1}\) を入力として，次のデータを予測するために \(\boldsymbol{H}^e\) のどこに注目すべきかを示す重み \(\alpha_{st}\) を生成します．
\(\alpha_{st}\) は Attention 重み (Attention weight) と呼ばれます．
Attention 層はこの重みを用いて次のデータを予測するための要約特徴量である，コンテキストベクトル \({c}_{s}\) を出力します．

コンテキストベクトル \({c}_{s}\) を現在の入力データ \(\boldsymbol{y}_s\) とともに RNN へ入力することで，適応的に \(\boldsymbol{H}^e\) の特徴を取り込んで次データを予測することが可能になります．

Attention の処理を特徴付けるのは \(e_{st} = score()\) という計算です．
この処理に関しては，第2.3項で説明します．

2.2 Luong RNN with Attention

文献[Luong'15]は，文献[Bahdanau'15]と同様に自然言語の翻訳タスク向けの RNN ベース Encoder-Decoder モデルを提案しています．

図3に文献[Luong'15]で提案しているモデルの処理構成を示します．

Encoder の処理構成は文献[Bahdanau'15]とほぼ同じですが，Decoderは下記の点で異なっています．

• Decoder-RNN の現在の出力 \(\boldsymbol{h}^d_{s}\) を Attention へ入力
• コンテキストベクトル \({c}_{s}\) は \(\boldsymbol{h}^d_{s}\) と共に線形変換層に入力
• 一つ前の線形変換層の出力 \(\tilde{\boldsymbol{h}}^d_{s-1}\) を，入力 \(\boldsymbol{y}_s\) とともに Decoder-RNN へ入力

Attention が過去の出力に依存しなくなることで，簡潔な処理構成になっていることが分かります．

2.3 Attentionの計算

第2.1項で，Attention の処理を特徴付けるのは \(e_{st} = score()\) の計算であると述べました．
本項では，文献[Bahdanau'15]と文献[Luong'15]で提案された計算処理を紹介したいと思います．

図4に Attention の処理構成を示します．

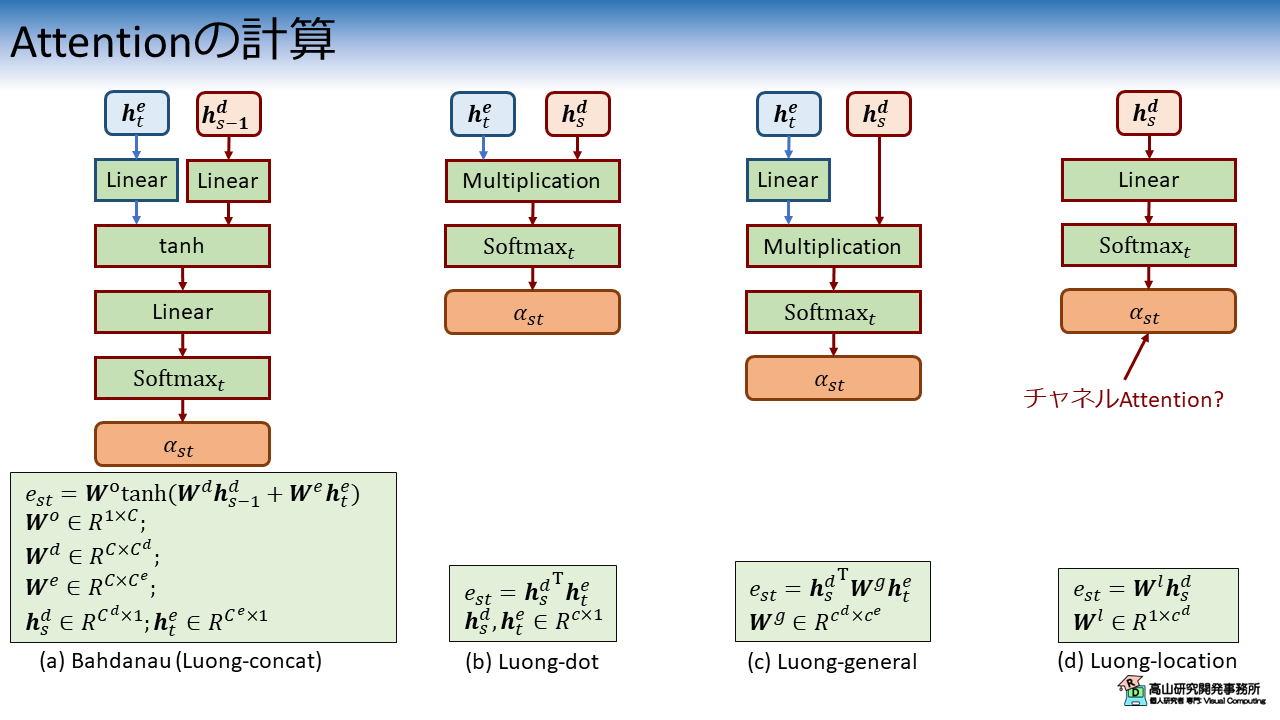
Additive attention (Concatenate attention)

図4(a) に示している処理は文献[Bahdanau'15]で提案されている手法で，現在では Additive attention と呼ばれています．
なお，この処理は文献[Luong'15]で "concat" と表記されている計算方式と同様です．

Additive attention では，重み付けの計算を線形変換層を用いて行います．
入出力の特徴量次元数の調整以外に，この処理構成が意味するところを解釈するのは難しいですが，線形変換層は翻訳性能を向上させようとしてより良いパラメータを学習します．
結果として予測に重要な箇所に対して高い応答値を出力するようになることが報告されています．

Dot-product attention

図4(b) に示している処理は文献[Luong'15]で "dot" と表記されている計算方式で，現在では Dot-product attention と呼ばれています．

この処理は入力の内積だけで構成されているため，学習パラメータが必要なく，かつ，高速な計算処理が可能です．
なお，内積を行う都合上，2入力の次元数は同一である必要があります．

ベクトルの内積がベクトルの大きさとなす角 (コサイン類似度) の積で定義されるため，この処理は2入力の類似性を評価していると解釈される場合があります．
この処理自体はそのような面があるとは思うのですが，前後に学習依存の複雑な変換が施されていることを見落とすと，結果の解釈に悩むことがあるので注意してください．

Multiplicative attention

図4(c) に示している処理は文献[Luong'15]で "general" と表記されている計算方式です．
(Multiplicative attention とも呼ばれます)

この処理では，片側の入力系列を線形変換して次元数を調整することで，Dot-product attention の制限を緩和しています．

Location-aware attention

図4(d) に示している処理は文献[Luong'15]で "location" と表記されている計算方式です．
(名称は定まっていないですが，"location-aware" や "location-based" という表記を見たことがあります)

---

【以前の説明】
この処理では，単一の入力系列を線形変換してスカラー化することで重みを計算します．
先日の記事で紹介した手法と同様の処理です．

---

上記のように説明していたのですが，attention への入力が \(\boldsymbol{h}_t^e\) であると勘違いしておりましたので訂正致します．

ただし，attention への入力が \(\boldsymbol{h}_s^d\) だとすると \(\alpha_{st}\) は1フレーム分しか無いので，Softmax の適用の仕方と コンテキストベクトルの求め方が不明ですね...
Softmax をチャネル方向に適用して，特徴次元の重み付けをするのでしょうか...?

• [Bahdanau'15]: D. Bahdanau, et al., "Neural Machine Translation by Jointly Learning to Align and Translate," Proc. of the ICLR, available here, 2015.
• [Luong'15]: M.-T. Luong, et al., "Effective Approaches to Attention-based Neural Machine Translation," Proc. of the EMNLP, available here, 2015.
• [Vaswani'17]: A. Vaswani, et al., "Attention Is All You Need," Proc. of the NIPS, available here, 2017.

2.4 Scaled-dot product attentionへの拡張

図5に示すように，Transformer の Scaled-dot production は Dot-production attention にスケーリング処理を追加した処理になります．

Transformer では行列演算を用いており，Multi-head 処理も追加されていることから，まるで違う処理に見えるかもしれませんが，Attention の計算自体は単純な改良が成されているだけです．

ここの "Scale" は\(\sqrt{c}\) で割って標準化する処理になります (\(c\) は入力の次元数です)．
内積 \(\boldsymbol{q}_s^T \boldsymbol{k}_t\) の計算結果は次元数に比例して大きくなります．
そのため，次元数が大きい場合は Softmax() 後の値が勾配の小さい領域 (1 や -1 付近) になる傾向があり，学習が上手く行かなくなります．
そこで標準化を行い値を小さくすることで，計算を安定化させています．

なお，標準化のパラメータ \(\sqrt{c}\) は下記のような仮定から導出されています．
ベクトル \(\boldsymbol{q}, \boldsymbol{k}\) を平均 \(0\)，分散 \(1\) の確率分布に従う，互いに独立な変数と仮定します．
このとき，内積 \(\boldsymbol{q}^T \boldsymbol{k} = \sum_{i=1}^c q_i k_i\) は 平均 \(0\)，分散 \(c\) の確率分布に従います．
(互いに独立なので，積の分散 \(\rightarrow\) 和の分散の順で求めると出てきます)

標準化は，平均で引いた後に標準偏差で割ることで，平均 \(0\)，分散 \(c\) の確率分布に従うようにデータを変換する操作です．
ここでは平均が \(0\) と仮定しているので，標準偏差 \(\sqrt{c}\) で割るだけで標準化の処理を行っていることになります．

2.5 Query, Key, Value について

余談ですが，図5(b) に示した Scaled dot product attention の入力 \(\boldsymbol{q}, \boldsymbol{k}\) は，それぞれ Query と Key と呼びます．
また，計算した Attention 重みは Value と呼ぶ値とかけ合わせます．

Query, Key, Value は情報検索の分野で使われる用語です．
例えば画像検索では，検索単語 (Query) を入力して，類似単語 (Key) を抽出し，Key に紐づいた画像 (Value) を提示します．

Scaled-dot product attention では，Query と Key の類似性に基づいて重みを計算し，その後重みに従って Value を抽出するのですが，Transformer の著者はこの処理を情報検索のアナロジーとして捉えているのが伺えて面白いですね．
(高山の感想です(^^;)．原著には用語について何も言及が無く，関連論文を全部読んだわけでもありません)

3. Multi-head self-attentionの内部動作

ここから先は，各処理を Step by step で説明していきながら，MHSAの特徴抽出の仕組みを解説していきます．

3.1 入力へ線形変換を適用

まず最初に，入力特徴量 \(\boldsymbol{Z}\) に対して，それぞれ異なる線形変換 \(\boldsymbol{W}^Q, \boldsymbol{W}^K, \boldsymbol{W}^V\) を適用します．

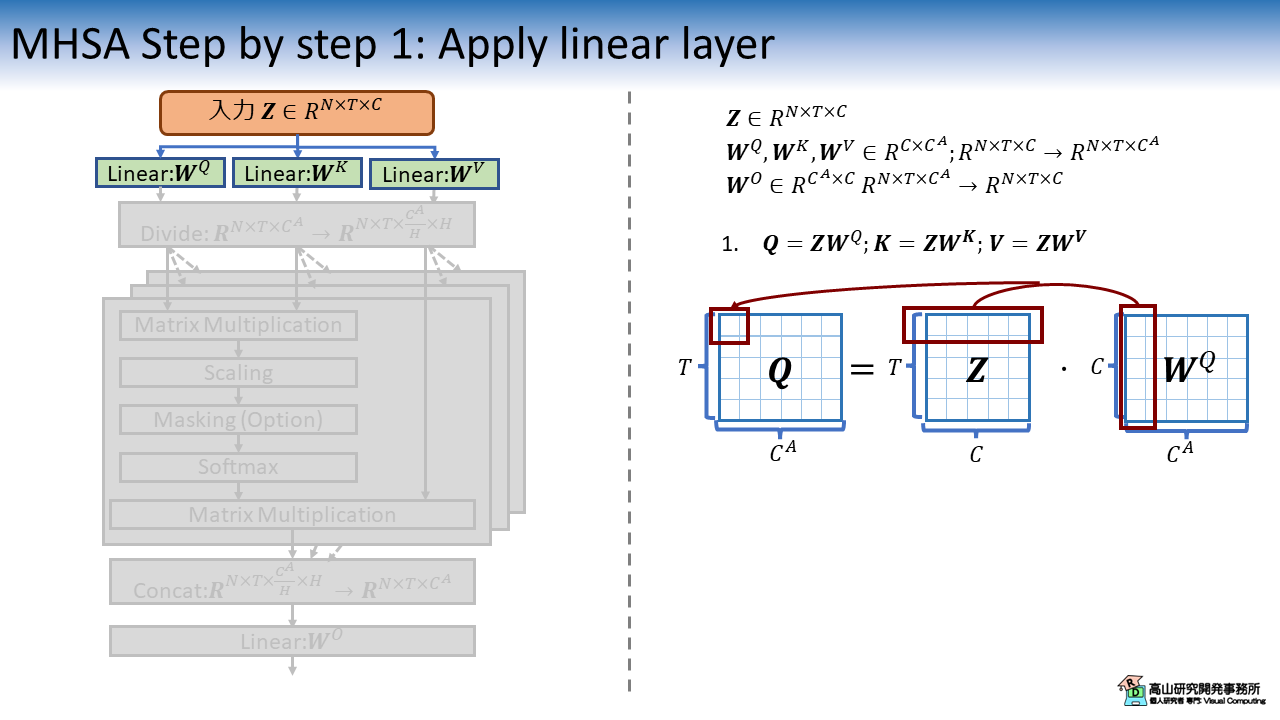
図中の赤四角に示すように，\(\boldsymbol{Z}\) の行，および \(\boldsymbol{W}\) の列の積和演算結果が出力行列の要素になります．

3.2 特徴量を次元毎に分割して各ヘッドに振り分け

MHSAでは Attention の計算を，特徴次元に沿って小分けにした特徴量に対して，それぞれ行います．
ここで，小分けにした特徴量に対して行われる計算処理郡はヘッドと呼ばれます．

各ヘッドでそれぞれ Attention を計算することで，入力系列内の複雑な関係性を捉えることが可能になります．

図3は特徴量を次元軸に沿って分割し，各ヘッドに振り分けている様子を示しています．

特徴次元に沿って均等に分割されるため，入力特徴量の次元数が \(C^A\)，ヘッド数が \(H\) だった場合は，各ヘッドに入力される特徴量の次元数は \(C^A/H\) になります．
この処理は \(Q, K, V\) 全てに対して行われます．

3.3 Scaled dot-product attention の適用

次に，第2.4項で説明した，Scaled dot-procuct attention を用いて Attention 重みを計算します．

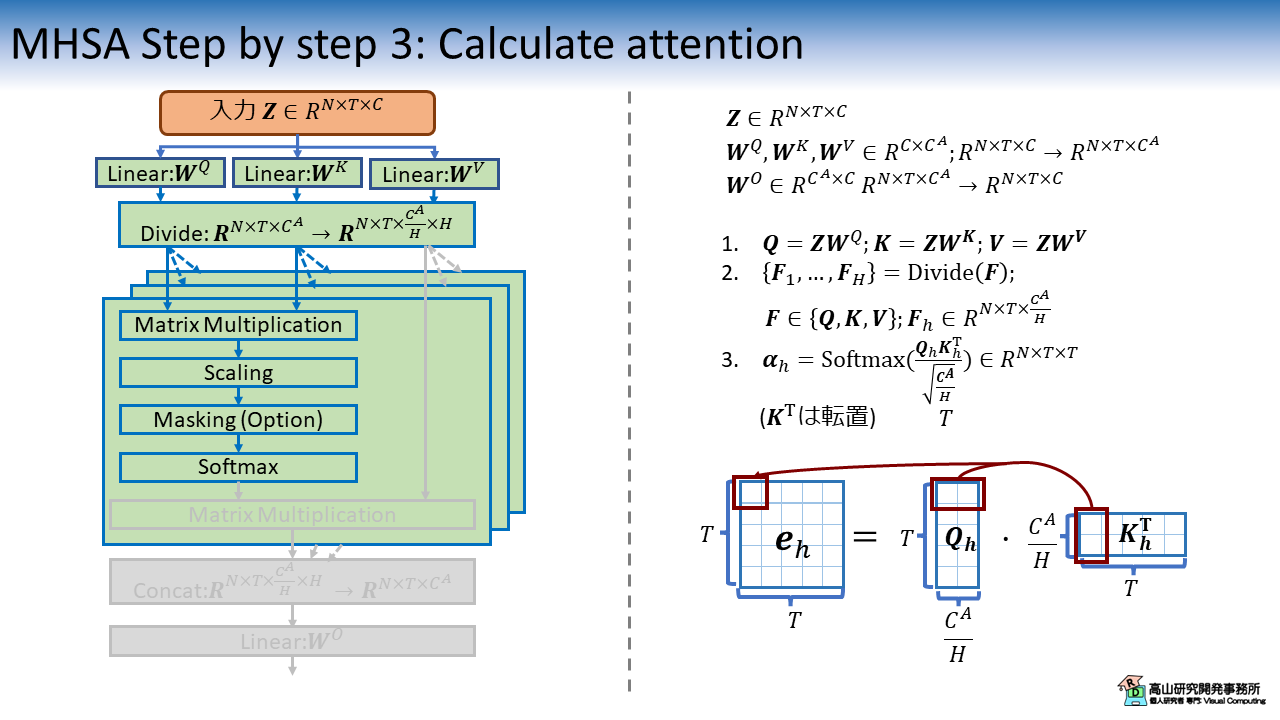
RNN では各時点でベクトルの内積計算をする必要がありましたが，Transformer では行列積を用いて全系列分の重みを同時に算出することができます．

図中の赤四角に示すように，行列積になっても計算の対応関係 (\(e_{st}=\boldsymbol{q}_s^T\boldsymbol{k}_t\)) は変わりません．

3.4 アテンションの適用

重みが計算できたら，重みと Value の行列積を計算します．

図中の赤四角に示すように，行列積の結果 \(\boldsymbol{O}\) の各行は第2.1項で説明したコンテキストベクトルに対応していることが分かります (\(\boldsymbol{O}_{tc} = \boldsymbol{\alpha}_t^T \boldsymbol{V}_c\))．

図10に，学習済みの Transformer モデルに孤立手話単語データを入力した際の，Attention 重みの例を示します．
この例では，第九回の記事で学習したモデルとデータセットを用いました．

この例では特に2番目と9番目のフレームの影響が強く，各フレームは該当フレームの特徴を取り込もうとしていることが分かります．
ただし，取り込む強度はレイヤおよびヘッド毎に異なっており，Multi-head 処理によって相補的な特徴抽出が行われていることが分かります．

3.5 特徴量の結合

Attention 適用後は特徴次元に沿って小分けに分割された特徴量を結合します．

この処理は特に難しい点はありません．

3.6 内部特徴量へ線形変換を適用

最後に，結合後の特徴量を線形変換して次元数を調整します．

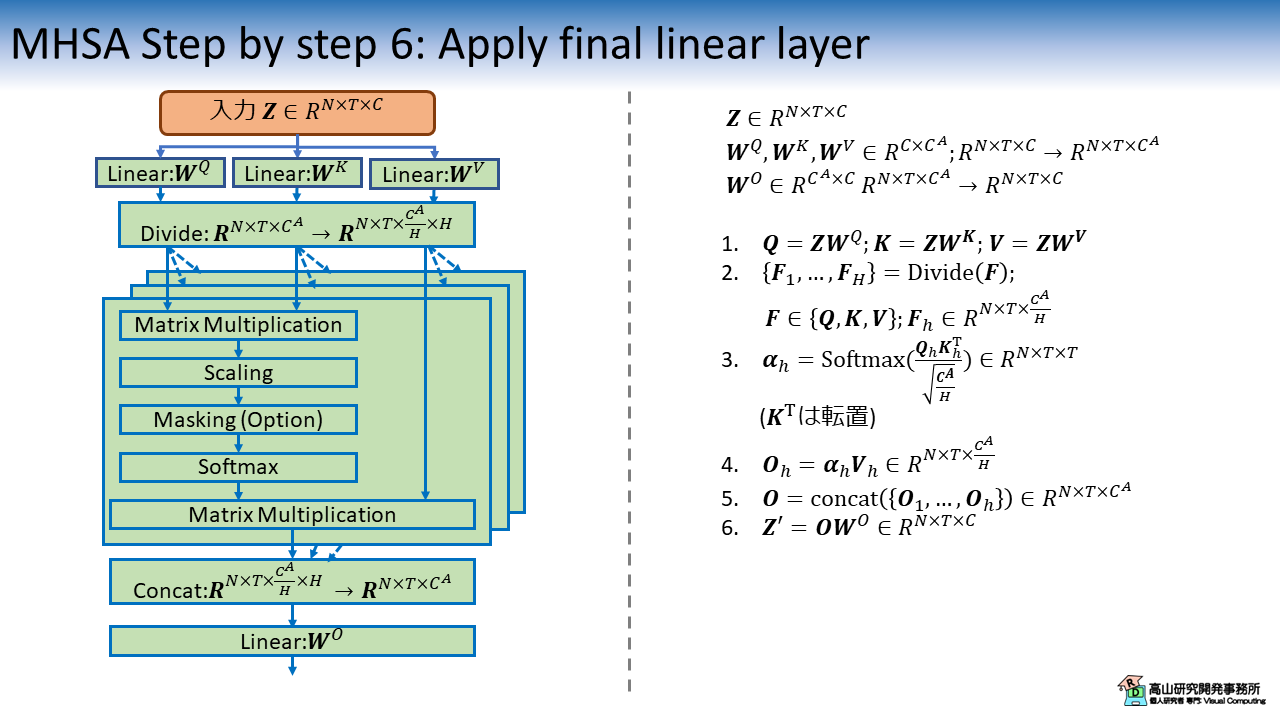
基本的には，入力と同じ次元数になるように設定します．

---

今回は Multi-head self-attention の動作，特徴について細かく説明しましたが，如何でしょうか?

今まで Encoder-Decoder モデルの説明は後回しにしていたのですが，Scaled dot-product attention の説明の都合上，触れざる負えませんでした．
これならば，以前 RNN を説明した時に Encoder-Decoder モデルも取り扱っていれば良かったと反省しています (^^;)．

RNN with Attention と Transformer の処理構成図が似ても似つかないため，2者は一見したところ大きく異なる処理のように見えます．
ですが，処理を丁寧に追っていくと結局のところ，素直な拡張の積み重ねで成り立っていることが分かって面白いですね．

今回紹介した話が，これから手話認識や深層学習を勉強してみようとお考えの方に何か参考になれば幸いです．